5. В треугольнике ABC Hзвестно, что AB-Вс -11 см. Середннный перпендикуляр к стороне В пересекает сторону DC в точке А. Найдите AC, если периметр
греуготника ВК С равен 50 см.

а) Прямые параллельны при условии коллинеарности векторов, т.е. при  условии пропорциональности координат этих векторов, а именно, если -1/4=2/х;  х=4*2/(-1)=-8

ответ при х=-8

б) при  условии перпендикулярности векторов, а это возможно, когда их скалярное произведение равно нулю, т .е. →m*→n=0; -1*4+4*х=0 ⇒4х=4; х=1

ответ при х=1

в) тупой угол прямые образуют при условии отрицательности скалярного произведения данных векторов, т.е.

→m*→n<0; -1*4+4*х<0;  4х<4; х<1; х∈(-∞;1)

ответ  при х∈(-∞;1)

Построение сечения: Назовем искомую плоскость MNK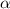 . Плоскости ABC и A1B1C1 параллельны и пересечены плоскостью  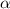, следовательно, линии пересечения параллельны. Значит,  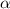пересекает А1В1С1 по прямой КF, параллельной MN. Значит, F - середина А1В1. Осталось соединить KF, FM, MN, NK. Искомое сечение - FKNM.

Доказательство: В треугольнике ABD MN-средняя линия, MN || BD. Т.к MN лежит в плоскости сечения MNK, а BD параллельна прямой MN, лежащей в плоскости сечения, ВD параллельна плоскости MNK, что и требовалось доказать.