8. вершины прямоугольного треугольника с катетами 3 см и 4 см лежат на сфере, радиус которой - 6,5 см. найдите расстояние от центра сферы до плоскости треугольника.
9. в правильную четырехугольную пирамиду, апофема которой равна 12 см, вписан шар. найдите радиус шара, если боковая грань пирамиды наклонена к плоскости основания под углом 60 °.
Объяснение:
По определению, две прямые параллельны, если существует плоскость в которой лежат две эти прямые, и они там параллельны. Отметим на данной прямой точки A и B. А точку обозначим как O. Пусть через точку О проходят две прямые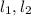
параллельные AB. Пусть 
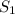-- плоскость, содержащая одновременно 
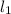и AB (эта плоскость существует из определения). Аналогично определяем плоскость 
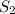. Заметим, что 
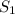и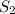 
проходят через точки O, A, B. Но по аксиоме через три точки, не лежащие на одной прямой проходит только одна плоскость. Значит плоскости 
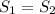= S совпадают. (назовём их общим именем S). Рассмотрим плоскость S: в ней лежат точки O, A, B и две прямые 
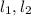. Причем, 
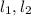проходят через точку O и параллельны AB. Но по аксиоме планиметрии (напомню, мы сейчас живем в плоскости S для которой выполнены все аксиомы планиметрии) через точку O может проходить лишь одна прямая, параллельная AB. Значит 
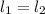, ч.т.д.
2. Пускай первый катет=x, тогда второй= x-10, а гипотенуза х+10. По теореме Пифагора получается два корня 0 и 40. 0 не подходит, тогда выходит, что первый катет = 40, второй 30, а гипотенуза 50. Периметр = 120см. Площадь прямоугольного треугольника = половине произведения катетов, то есть 60см квадратных.
3. Если треугольник равнобедренный, то по формуле площади S=1/2ah, где а -боковая сторона, h - высота, получается, что 48=1/2•а•8, отсюда а=12.