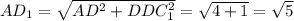А) х = ?; б) х = ? если AD и
BE - биссектрисы, BAC = 64°, ABC = 96°​

Задача  не требует рисунка, т.к. проверяются только формулы.

1. Если высота ромба х см, то сторона ромба, лежащего в основании, равна х+0.5х=1.5х.

2. Сумма стороны и высоты 1.5х+х=7.5, откуда х=7.5/2.5=3/см/, высота 3см, сторона ромба 1.5*3=4.5/см/

3. Площадь полной поверхности состоит из двух площадей оснований ромба и площади боковой поверхности, равной произведению периметра основания на высоту. т.е. 2S₁+S₂=S; где S - площадь полной поверхности,  - S₁-площадь основания, S₂ -площадь боковой поверхности.

S₁=4.5*3=13.5/см²/; 2S₁=27/см²/;S=107 см²;

4. S₂=(S-2S₁)=107-27=80/см²/, тогда высота  параллелепипеда равна 80/(4.5*4)=40/9

5. Объем равен произведению площади основания на высоту параллелепипеда, т.е. 13.5*40/9=60/см³/

AC₁=2

AD₁=√5

Объяснение:

1. Рассмотрим ΔАВС (см. рис. 1). Он равнобедренный с АВ=ВС=1 и ∠В=120° (как внутренний угол правильного шестиугольника). Опустим  высоту ВО на АС. Получили два равных прямоугольных ΔАВО = ΔСВО с углами 60°,  30° и 90° (т.к. ВО в равнобедренном тр-ке есть биссектрисой).

По теореме Пифагора,

тогда АС=АО*2=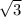

Рассмотрим ΔACC₁ (см. рис. 3). Он прямоугольный с двумя известными катетами

АС=√3, CC₁=1. Гипотенуза АС₁ является искомой величиной.

По теореме Пифагора: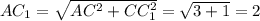

2. Рассмотрим ΔACD. Он прямоугольный с двумя известными катетами

АС=√3, CD=1 (см. рис. 2). Найдем гипотенузу АD.

Рассмотрим ΔADD₁ (см. рис. 4). Он прямоугольный с двумя известными катетами

АD=2, DD₁=1. Гипотенуза АD₁ является искомой величиной.

По теореме Пифагора: