Имеется есть 10 квадратных карточек, стороны которых равны соответственно 10 единиц, 9, 8 и т.д. до 1 единицы. Карточки с четными сторонами, черные, а остальные карточки белые. Положим на стол самую большую карточку (это черная карточка со стороной 10 единиц). Потом на нее (так, чтобы она лежала в левом верхнем углу черной карточки) положим белую карточку со стороной 9 единиц (см. рис. а). Затем на нее (в левый нижний угол) положим черную карточку со стороной 8 (рис. б). На нее (в правый нижний угол) кладем следующую по размеру карточку. Продолжим этот процесс далее, причем положения карточек как бы “закручиваются’’ внутрь против часовой стрелки. Вопрос: какой рисунок получится после выкладывания последней карточки?
Немного отвлечемся от задачек, чтобы вы сразу не бросались читать решения, а немного сами подумали над ними. Впрочем, как всегда ;) .
Стивен Барр — американский писатель и любитель математики. К математике Барр обратился довольно поздно. Он заинтересовался задачами моделирования сложных поверхностей, что и привело к тому, что он начал ей заниматься. Его интерес подерживал Мартин Гарднер. В США Барр издал три книги, которые имели довольно большой успех, возможно, даже больший, чем его художественные произведения.
А теперь приведу решения задач.
1. Произведение в знаменателе — это разность квадратов:
Объяснение: в листке решение биквадратного уравнения
1. Стороны должны составить геометрическую составить геометрическую прогрессию. Пусть q >1 - знаменатель прогрессии
Тогда катет- а, другой катет - qa гипотенуза q²a
Это должно подчиняться теореме Пифагора
a² +q²a² = q⁴a² Здесь а сокращается (это говорит о том, что выбор длины первого катета на имеет значения и таких треугольников бесконечное множество) и получаем биквадратное уравнение.
q⁴ - q - 1 = 0 Я считаю, что человек, которому дают такие задания достаточно продвинут и умеет решать биквадратные уравнения. Лень писать, поэтому сразу решение.Если возьмем
сторону а равной 1, то второй катет равен
q = а гипотенуза
q² =
Тогда угол sinα = 1/q = = 0.618 Это в в принципе решение, но все же найдем угол
Имеется есть 10 квадратных карточек, стороны которых равны соответственно 10 единиц, 9, 8 и т.д. до 1 единицы. Карточки с четными сторонами, черные, а остальные карточки белые. Положим на стол самую большую карточку (это черная карточка со стороной 10 единиц). Потом на нее (так, чтобы она лежала в левом верхнем углу черной карточки) положим белую карточку со стороной 9 единиц (см. рис. а). Затем на нее (в левый нижний угол) положим черную карточку со стороной 8 (рис. б). На нее (в правый нижний угол) кладем следующую по размеру карточку. Продолжим этот процесс далее, причем положения карточек как бы “закручиваются’’ внутрь против часовой стрелки. Вопрос: какой рисунок получится после выкладывания последней карточки?
Немного отвлечемся от задачек, чтобы вы сразу не бросались читать решения, а немного сами подумали над ними. Впрочем, как всегда ;) .
Стивен Барр — американский писатель и любитель математики. К математике Барр обратился довольно поздно. Он заинтересовался задачами моделирования сложных поверхностей, что и привело к тому, что он начал ей заниматься. Его интерес подерживал Мартин Гарднер. В США Барр издал три книги, которые имели довольно большой успех, возможно, даже больший, чем его художественные произведения.
А теперь приведу решения задач.
1. Произведение в знаменателе — это разность квадратов:
\[1234567890\cdot 1234567892=(1234567891-1)\cdot(1234567891+1)=1234567891^2-1,\]
откуда знаменатель сразу находится — он равен 1. Соответственно, вся дробь равна числителю, и это 1234567890.
2. Получится черный квадрат, на котором расположена белая спираль, состоящая из квадратиков, которая закручивается внутрь по часовой стрелке:
Объяснение:
ответ: 38° и 52°
Объяснение: в листке решение биквадратного уравнения
1. Стороны должны составить геометрическую составить геометрическую прогрессию. Пусть q >1 - знаменатель прогрессии
Тогда катет- а, другой катет - qa гипотенуза q²a
Это должно подчиняться теореме Пифагора
a² +q²a² = q⁴a² Здесь а сокращается (это говорит о том, что выбор длины первого катета на имеет значения и таких треугольников бесконечное множество) и получаем биквадратное уравнение.
q⁴ - q - 1 = 0 Я считаю, что человек, которому дают такие задания достаточно продвинут и умеет решать биквадратные уравнения. Лень писать, поэтому сразу решение.Если возьмем
сторону а равной 1, то второй катет равен
q =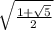 а гипотенуза
а гипотенуза
q² =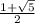
Тогда угол sinα = 1/q =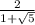 = 0.618 Это в в принципе решение, но все же найдем угол
= 0.618 Это в в принципе решение, но все же найдем угол
α = arksin(0,618) = 38°
Тогда второй угол 90°-38° = 52°