а) Нет такого шестиугольника
b) Внешний угол семиугольника равен . Сумма внешних углов семиугольника равна 360°.
Объяснение:
а) сумма углов выпуклого многоугольника равна по формуле
S=180°(n-2)
Где n - количество углов многоугольника. Здесь n=6.
S=180°(6-2)
S=180°*4
S=720° - сумма внутренних углов шестиугольника.
Просуммируем 6 углов
10°+50°+140°+175°+185°+200°=200°+175°+185°+200°=400°+360°=760°
То есть такого выпуклого шестиугольника не существует в Евклидовой геометрии.
b) У правильного семиугольника сумма внутренних углов равна
S=180°(7-2)
S=180°*5
S=900°
- внутренний угол семиугольника.
Внешний угол равен
А сумма внешних углов равна
.
Площадь квадрата равна 8 ед²
Дано
Окружность
АBCDEF- шестиугольник вписанный
KLMN- квадрат вписанный.
SABCDEF=6√3 ед²
SKLMN=?
Решение
Шестиугольник состоит из 6 равносторонних треугольников.
Найдем площадь одного треугольника.
S∆ABO=SABCDEF/6=6√3/6=√3 eд² площадь одного треугольника.
Из формулы равностороннего треугольника
S=a²√3/4, где а -сторона треугольника.
Найдем сторону треугольника.
а=√(4S/√3)=√(4√3/√3)=2 ед сторона треугольника
а=АО=R=2ед.
КМ диагональ квадрата равна диаметру окружности.
КМ=2*АО=2*2=4 ед. диагональ квадрата.
Из формулы нахождения диагонали квадрата
КМ=КN*√2.
Найдем сторону квадрата.
КN=KM/√2=4/√2=2√2 сторона квадрата.
SKLMN=KN²=(2√2)²=4*2=8 ед² площадь квадрата
а) Нет такого шестиугольника
b) Внешний угол семиугольника равен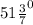 . Сумма внешних углов семиугольника равна 360°.
. Сумма внешних углов семиугольника равна 360°.
Объяснение:
а) сумма углов выпуклого многоугольника равна по формуле
S=180°(n-2)
Где n - количество углов многоугольника. Здесь n=6.
S=180°(6-2)
S=180°*4
S=720° - сумма внутренних углов шестиугольника.
Просуммируем 6 углов
10°+50°+140°+175°+185°+200°=200°+175°+185°+200°=400°+360°=760°
То есть такого выпуклого шестиугольника не существует в Евклидовой геометрии.
b) У правильного семиугольника сумма внутренних углов равна
S=180°(7-2)
S=180°*5
S=900°
Внешний угол равен
А сумма внешних углов равна
Площадь квадрата равна 8 ед²
Объяснение:
Дано
Окружность
АBCDEF- шестиугольник вписанный
KLMN- квадрат вписанный.
SABCDEF=6√3 ед²
SKLMN=?
Решение
Шестиугольник состоит из 6 равносторонних треугольников.
Найдем площадь одного треугольника.
S∆ABO=SABCDEF/6=6√3/6=√3 eд² площадь одного треугольника.
Из формулы равностороннего треугольника
S=a²√3/4, где а -сторона треугольника.
Найдем сторону треугольника.
а=√(4S/√3)=√(4√3/√3)=2 ед сторона треугольника
а=АО=R=2ед.
КМ диагональ квадрата равна диаметру окружности.
КМ=2*АО=2*2=4 ед. диагональ квадрата.
Из формулы нахождения диагонали квадрата
КМ=КN*√2.
Найдем сторону квадрата.
КN=KM/√2=4/√2=2√2 сторона квадрата.
SKLMN=KN²=(2√2)²=4*2=8 ед² площадь квадрата