см.
Проведём отрезки и .
=======================================================
и - радиусы данной сферы ⇒ они равны.
⇒ - равнобедренный, где - расстояние от точки до прямой и высота равнобедренного
Высота, проведённая из вершины равнобедренного треугольника к основанию равнобедренного треугольника, является биссектрисой и медианой.
⇒ - высота, медиана и биссектриса.
см, так как - медиана.
- прямоугольный, так как - высота.
Найдём радиус по теореме Пифагора .
Итак, радиус данной сферы = см.
рассмотрим треугольник ahc-прямоуг., равнобедренный ah=ch=x, ac^2=ah^2+ch^2,
2^2=x^2+x^2
4=2x^2
2=x^2
x=корень из 2
рассмотрим треугольник chb, по теореме пифагора
cb^2=ch^2+hb^2
cb^2= 3^2+(корень из 2)^2=9+2=11
cb= корень из 11
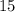см.
Объяснение:Проведём отрезк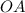и
и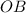 
.
=======================================================
⇒
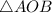- равнобедренный, где 
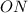- расстояние от точки 
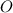до прямой 
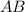и высота равнобедренного
Высота, проведённая из вершины равнобедренного треугольника к основанию равнобедренного треугольника, является биссектрисой и медианой.
⇒
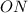- высота, медиана и биссектриса.
Найдём радиус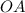
по теореме Пифагора 
.
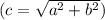Итак, радиус данной сферы =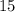
см.
рассмотрим треугольник ahc-прямоуг., равнобедренный ah=ch=x, ac^2=ah^2+ch^2,
2^2=x^2+x^2
4=2x^2
2=x^2
x=корень из 2
рассмотрим треугольник chb, по теореме пифагора
cb^2=ch^2+hb^2
cb^2= 3^2+(корень из 2)^2=9+2=11
cb= корень из 11