Бассейн для плавания имеет форму прямоугольного параллелепипеда с размерами 50м*20м*3м. Определить за какое время бассейн наполнится водой на высоту 2,8 м, если за 1 минуту в бассейн поступает 6,7 м3 воды.
Треугольник АВС, угол С прямой, СМ - медиана, СМ = 25, СН - высота, СН = 24.
Ясно, что АС = 2*СМ = 50. Площадь АВС равна 24*50/2 = 600;
Треугольник СНМ - прямоугольный треугольник с катетом 24 и гипотенузой 25, то есть это Пифагоров треугольник (7,24,25). МН = 7.
Поэтому АН = АМ + МН = 25 + 7 = 32, ВН = 25 - 7 = 18.
Теперь можно сосчитать по теореме Пифагора катеты, но это очень скучно.:)
Рассмотрим внимательнее треугольники АСН и ВСН.
Тр-к АСН имеет катеты 24 и 32, и легко видеть, что это треугольник, подобный "египетскому" со сторонами (3,4,5) с коэффициентом подобия 8. Поэтому у этого треугольника стороны (24,32,40). АС = 40.
Тр-к ВСН подобен АСН, то есть это тоже "египетский" треугольник, его стороны (18,24,30). ВС = 30.
Треугольник АВС тоже подобен АСН, и он тоже "египетский", его гипотенуза 50, поэтому это треугольник со сторонами (30,40,50). :))) (по одной гипотенузе я нашел все стороны :)))
Приметр равен 30 + 40 + 50 = 120.
Я обращаю внимание на то, что "экономничное" решение на много короче. После нахождения АН = 32, констатируется подобие АВС и АСН,
то есть СВ/АВ = СН/АН = 24/32 = 3/4. Это - отношение катетов "египетского" треугольника, поэтому АВС это треугольник (30,40,50) с периметром 120. Это все.
В прямоугольном треугольнике на середине гипотенузы лежит центр описанной окружности, то медиана является также радиусом описанной окружности, то гипотенуза равна 50 см.
Площадь данного треугольника S= , где а - гипотенуза, h - высота, проведенна к гипотенузе
S= см^2
Высота, проведенная к гипотенузу есть среднее пропорциональное между проекциями катетов на гипотенузу, т.е. , где с и d - проекции катетов на гипотенузу
Пусть одна проекция равна х см, то вторая (50-х) см. то подставляя в формулу, имеем:
576=50x-
x1=32, x2=18
Значит проекции катетов на гипотенузу 32 см и 18 см.
Треугольник АВС, угол С прямой, СМ - медиана, СМ = 25, СН - высота, СН = 24.
Ясно, что АС = 2*СМ = 50. Площадь АВС равна 24*50/2 = 600;
Треугольник СНМ - прямоугольный треугольник с катетом 24 и гипотенузой 25, то есть это Пифагоров треугольник (7,24,25). МН = 7.
Поэтому АН = АМ + МН = 25 + 7 = 32, ВН = 25 - 7 = 18.
Теперь можно сосчитать по теореме Пифагора катеты, но это очень скучно.:)
Рассмотрим внимательнее треугольники АСН и ВСН.
Тр-к АСН имеет катеты 24 и 32, и легко видеть, что это треугольник, подобный "египетскому" со сторонами (3,4,5) с коэффициентом подобия 8. Поэтому у этого треугольника стороны (24,32,40). АС = 40.
Тр-к ВСН подобен АСН, то есть это тоже "египетский" треугольник, его стороны (18,24,30). ВС = 30.
Треугольник АВС тоже подобен АСН, и он тоже "египетский", его гипотенуза 50, поэтому это треугольник со сторонами (30,40,50). :))) (по одной гипотенузе я нашел все стороны :)))
Приметр равен 30 + 40 + 50 = 120.
Я обращаю внимание на то, что "экономничное" решение на много короче. После нахождения АН = 32, констатируется подобие АВС и АСН,
то есть СВ/АВ = СН/АН = 24/32 = 3/4. Это - отношение катетов "египетского" треугольника, поэтому АВС это треугольник (30,40,50) с периметром 120. Это все.
В прямоугольном треугольнике на середине гипотенузы лежит центр описанной окружности, то медиана является также радиусом описанной окружности, то гипотенуза равна 50 см.
Площадь данного треугольника S=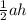
, где а - гипотенуза, h - высота, проведенна к гипотенузе
S=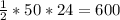
см^2
Высота, проведенная к гипотенузу есть среднее пропорциональное между проекциями катетов на гипотенузу, т.е.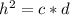
, где с и d - проекции катетов на гипотенузу
Пусть одна проекция равна х см, то вторая (50-х) см. то подставляя в формулу, имеем:
576=50x-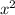
x1=32, x2=18
Значит проекции катетов на гипотенузу 32 см и 18 см.
По т. Пифагора найдем катеты:
катет1=[tex]\sqrt{24^{2}+32^{2}}=40
катет2=[tex]\sqrt{24^{2}+18^{2}}=30
P=50+40+30=120 см