Биссектрисы углов A и B треугольника ABC пересекаются в точке M. Найдите
∠
AMB, если
∠
С = 86
0
.

Показать ответ

Ответ:

HateLove7

23.03.2022 17:50

1.P=2(a+b), пусть а=х, тогда
30=2х+8х
30=10х
х=3, первая сторона
4*3=12м, вторая сторона
ответ: 3см, 3см, 12см, 12см
3.Биссектриса угла А отсекает от прямоугольника равнобедренный треугольник АВЕ. Значит АВ=ВЕ=7см, ВС=7+3=10см. Периметр равен 2*(7+10)=34см.
ответ: периметр = 34см
4.Меньшая диагональ АС=24см
Угол А=60°
Меньшая диагональ делит ромб на 2 треугольника: АВС и АСD
Так как угол А= углу D= 60° , то треугольники равносторонние и сторона ромба =24 см
5.Периметр= 4а
а=46:4=11,5см
Площадь= а^2=11,5×11,5=132,25см^2

0,0(0 оценок)

Ответ:

marinka02jkjk

20.01.2022 23:47

$1) \ x = \sqrt{13} \\2) \ x = \sqrt{21} \\3) x_1 = 7, x_2=x_3 = 7\sqrt{2}$

Объяснение:

Обозначим неизвестные отрезки за x

1) неизвестный отрезок является гипотенузой прямоугольного треугольника:

$x = \sqrt{3^2+2^2} = \sqrt{9+4} = \sqrt{13}$

2) неизвестный отрезок является высотой, проведённой к основанию, в равнобедренном треугольнике. Как известно, высота, проведённая к основанию, в равнобедренном треугольнике является также медианой и биссектрисой. Следовательно неизвестный отрезок делит основание пополам и является катетом в прямоугольном треугольнике с гипотенузой равной 5 и катетом равным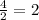 $\frac{4}{2} = 2$ :

$x = \sqrt{5^2 - 2^2} = \sqrt{25 - 4} = \sqrt{21}$

3) Здесь имеется три неизвестных отрезка, два из которых равны.

Начнём с высоты, опять же она проведена к основанию в равнобедренном треугольнике, а значит является и медианой и биссектрисой. А медиана проведённая к гипотенузе в прямоугольном треугольнике равна половине гипотенузы:

$x_1 = \frac{14}{2} = 7$

Нам известно, что оставшиеся неизвестные отрезки являются катетами в прямоугольном треугольнике и что они равны. Нам известна гипотенуза этого треугольника:

$x_2 = x_3,\\\sqrt{x_2^2+x_3^2} = 14 \\\sqrt{2x_2^2} = 14\\x_2\sqrt{2} = 14\\x_2 = \frac{14}{\sqrt{2} } = \frac{14\sqrt{2} }{2} = 7\sqrt{2}$