Через середину высоты равнобедренного треугольника проведены две прямые, соединяющие её с вершинами основания. какую часть площади треугольника составляют каждая из 6-ти частей, на которые эти две прямые разделяют треугольники?

Показать ответ

Ответ:

alah200

26.07.2020 09:26

Дано: ΔABC : AB=BC; BH⊥AC; BO=OH

Найти: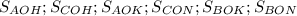 $S_{AOH}; S_{COH}; S_{AOK}; S_{CON}; S_{BOK}; S_{BON}$

$S_{ABC}=\dfrac{AC\cdot BH}{2}$

ΔABC - равнобедренный, высота BH является медианой и биссектрисой

⇒ AH = HC ⇒ ΔABH = ΔCBH - по двум катетам. Дальше можно рассматривать только одну половинку равнобедренного треугольника.

$S_{AOH} = \dfrac{AH\cdot OH}{2}=\dfrac{\frac{AC}{2}\cdot \frac{BH}{2}}{2}=\dfrac{1}{4}\cdot \dfrac{AC\cdot BH}{2}=\dfrac{1}{4}\cdot S_{ABC}\\ \\ \boxed{\boldsymbol{S_{AOH} =S_{COH} =\dfrac{1}{4}\cdot S_{ABC}}}$

$S_{AOB}=\dfrac{1}{2}\cdot S_{ABC}-S_{AOH}=\\ \\~~~~~~~~~= \dfrac{1}{2}\cdot S_{ABC}-\dfrac{1}{4}\cdot S_{ABC}=\dfrac{1}{4}\cdot S_{ABC}$

У треугольников AOK и BOK одинаковая высота OM. Поэтому их площади будут пропорциональны основаниям AK и KB. Чтобы найти отношение АК:КВ, достроим треугольник ABH до прямоугольника ALBH. LB=AH; AL=BH; LB║AH; AL║BH

∠AKL=∠OKB - вертикальные углы.

∠LAK=∠OBK - накрест лежащие углы при AL║BH и секущей АВ. ⇒

ΔAKL ~ ΔBKO подобны по двум углам:

$\dfrac{AK}{KB}=\dfrac{AL}{BO}=\dfrac{2BO}{BO}=2~~~\Rightarrow~~~\boldsymbol{AK=2KB}~~~\Rightarrow\\ \\ \\S_{AOK}=\dfrac{AK\cdot OM}{2}=\dfrac{2KB\cdot OM}{2}=2\cdot S_{BOK} \\ \\ S_{AOB}=\dfrac{1}{4}\cdot S_{ABC}\\ \\ S_{AOB}=S_{AOK}+S_{BOK}=\dfrac{1}{4}\cdot S_{ABC}\\ \\ 2\cdot S_{BOK}+S_{BOK}=\dfrac{1}{4}\cdot S_{ABC}\\ \\ 3\cdot S_{BOK}=\dfrac{1}{4}\cdot S_{ABC}~~~\Rightarrow~~~S_{BOK}=\dfrac{1}{12}\cdot S_{ABC}\\ \\ \boxed{\boldsymbol{S_{BOK}=S_{BON}=\dfrac{1}{12}\cdot S_{ABC}}}$

$S_{AOK}=2\cdot S_{BOK}=2\cdot \dfrac{1}{12}\cdot S_{ABC}=\dfrac{1}{6}\cdot S_{ABC}\\ \\ \\ \boxed{\boldsymbol{S_{AOK}=S_{CON}=\dfrac{1}{6}\cdot S_{ABC}}}$