Чи можуть дві різні площини мати 3 спілтні точки, що не лежать на одній прямій

Показать ответ

Ответ:

iraapukhtina7

26.04.2020 19:19

Объяснение:

$\displaystyle y=(2+x^2)e^{-x^2}=\frac{1+x^2}{e^{x^2}}$

1. ОДЗ: х ∈ R

или х ∈ (-∞; +∞)

2. Четность, нечетность.

$\displaystyle y(-x)=\frac{2+(-x)^2}{e^{(-x)^2}} =\frac{2+x^2}{e^{x^2}}$

y(-x) = y(x) ⇒ четная

3. Пересечение с осями.

1) х = 0 ⇒ у = 2

2) у > 0 ⇒ ось 0х не пересекает.

4. Асимптоты.

1) Вертикальных асимптот нет.

2) Наклонная: y = kx + b

$\displaystyle k = \lim_{x \to ^+_-\infty} \frac{2+x^2}{x*e^{x^2}} =0\\\\b= \lim_{x \to ^+_-\infty} (\frac{2+x^2}{e^{x^2}}-0*x)=0$

y = 0 - горизонтальная асимптота.

5. Возрастание, убывание, экстремумы.

Найдем производную:

$\displaystyle y'=\frac{2x*e^{x^2}-(2+x^2)*e^{x^2}*2x}{e^{2x^2}} =\\\\=\frac{2x*e^{x^2}(1-2-x^2)}{e^{2x^2}}=-\frac{2x(1+x^2)}{e^{x^2}}$

Приравняем к 0 и найдем корни:

$\displaystyle -2x(1+x^2)\\\\x=0$

Найдем знаки производной на промежутках. Если "+" - возрастает, "-" - убывает.

$\displaystyle x_{max}=0;\;\;\;y(0)=2\\$

Возрастает при х ∈ (-∞; 0]

Убывает при х ∈ [0; +∞)

См. рис.

6. Выпуклость, вогнутость.

Найдем производную второго порядка.

$\displaystyle y''=(-\frac{2x+2x^3}{e^{x^2}} )'=-\frac{(2+6x^2)*e^{x^2}-(2x+2x^3)*e^{x^2}*2x}{e^{2x^2}} \\\\=-\frac{e^{x^2}(2+6x^2-4x^2-4x^4)}{e^{2x^2}} =\frac{2(2x^4-x^2-1)}{e^{x^2}}$

Приравняем к 0 и найдем корни:

Заменим переменную:

$\displaystyle x^2=t;\;\;\;t\geq 0$

$\displaystyle 2t^2-t-1=0\\\\t_{1,2}=\frac{1^+_-\sqrt{1+8} }{4} =\frac{1^+_-3}{4} \\\\t_1 = 1;\;\;\;t_2=-\frac{1}{2}$

t > 0 ⇒ x² = 1

x₁ = 1; x₂=-1

Найдем знаки второй производной на промежутках.

( См. рисунок.)

x перегиба = ±1

$\displaystyle y(^+_-1)=\frac{2+1}{e}\approx 1,1$

При х ∈ (-∞; -1] ∪ [1; +∞) - вогнута;

при х ∈ [-1; 1] - выпукла.

Строим график.

очень Нужно сделать исследование функции и построить график

0,0(0 оценок)

Ответ:

Aryzhaн

08.06.2023 19:16

$\boxed{HK \approx 8,9}$

Объяснение:

Дано: ABCD - параллелограмм, ∠BAD < 90°, AH ⊥ BC, AK ⊥ CD, AB = 5,

AC = 15, AH = 3

Найти: HK - ?

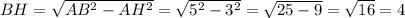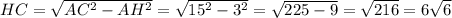Решение: Так как по условию AH ⊥ BC, то угол ∠AHC = 90°, тогда для прямоугольного треугольника ΔAHB по теореме Пифагора: $BH = \sqrt{AB^{2} - AH^{2}} = \sqrt{5^{2} - 3^{2}} = \sqrt{25 - 9} = \sqrt{16} = 4$ . Также так как угол ∠AHC = 90°, то треугольник ΔAHC - прямоугольный. Рассмотрим прямоугольный треугольник ΔAHC. По теореме Пифагора: $HC = \sqrt{AC^{2} - AH^{2}} = \sqrt{15^{2} - 3^{2}} = \sqrt{225 - 9} = \sqrt{216} = 6\sqrt{6}$ .

По основному свойству отрезка: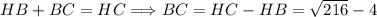 $HB + BC = HC \Longrightarrow BC = HC - HB = \sqrt{216} - 4$

По свойствам параллелограмма (ABCD) его противоположные стороны равны, тогда AB = CD = 5,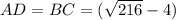 $AD = BC = (\sqrt{216} - 4 )$ .

По формуле площади параллелограмма:

$\displaystyle \left \{ {{S_{ABCD} = AK \cdot CD} \atop {S_{ABCD} = AH \cdot BC}} \right \Longrightarrow AK \cdot CD = AH \cdot BC \Longrightarrow AK = \dfrac{AH \cdot BC}{CD} =$

$= \dfrac{3 \cdot (\sqrt{216} - 4)}{5} = \dfrac{3\sqrt{216} - 12}{5}$ . Рассмотрим треугольник прямоугольный (так как по условию AK ⊥ CD, то угол ∠AKC = 90°) треугольник ΔAKC. По теореме Пифагора: $CK = \sqrt{AC^{2} - AK^{2}} = \sqrt{15^{2} - \left (\dfrac{3\sqrt{216} - 12}{5} \right)^{2}}= \sqrt{225 - \dfrac{1944 - 432\sqrt{6} +144}{25} }=$ $= \sqrt{\dfrac{5625}{25} - \dfrac{1944 - 432\sqrt{6} +144}{25} }= \sqrt{ \dfrac{5625-1944 - 432\sqrt{6} +144}{25} } =$

$=\sqrt{ \dfrac{3825 - 432\sqrt{6} }{25} }$ . По формуле площади параллелограмма:

$\displaystyle \left \{ {{S_{ABCD} = BC \cdot CD \cdot \sin \angle HCK} \atop {S_{ABCD} = AH \cdot BC}} \right \Longrightarrow BC \cdot CD \cdot \sin \angle HCK = AH \cdot BC \Longrightarrow$

$\sin \angle HCK = \dfrac{AH \cdot BC}{BC \cdot CD} = \dfrac{AH}{CD} = \dfrac{3}{5} = 0,6$ . По свойствам параллелограмма его противоположные углы равны, тогда ∠BAD = ∠BCD, так как по условию ∠BAD < 90°, то и угол ∠BCD < 90°, следовательно

cos ∠BCD > 0. По основному тригонометрическому тождеству:

$\sin^{2} \angle HCK + \cos^{2} \angle HCK = 1 \Longrightarrow \cos \angle HCK = \sqrt{1 - \sin^{2} \angle HCK} =$

$= \sqrt{1 - (0,6)^{2}} = \sqrt{1 - 0,36} = \sqrt{0,64} = 0,8$ . По теореме косинусов для треугольника ΔHCK: $HK = \sqrt{HC^{2} + CK^{2} - 2 \cdot HC \cdot CK \cdot \cos \angle HCK} =$

$= \sqrt{(\sqrt{216} )^{2} + \left (\sqrt{ \dfrac{3825 - 432\sqrt{6} }{25} } \right )^{2} - 2 \cdot \sqrt{216} \cdot \sqrt{ \dfrac{3825 - 432\sqrt{6} }{25} }\cdot 0,8 } =$

$= \sqrt{216 + \dfrac{3825 - 432\sqrt{6} }{25} - 1,6 \cdot \sqrt{216} \cdot\dfrac{3\sqrt{425 - 48\sqrt{6} } }{5} } =$

$= \sqrt{ \dfrac{5400 + 3825 - 432\sqrt{6} }{25} - \dfrac{28,8\sqrt{6} \sqrt{425 - 48\sqrt{6} } }{5} } =$

$= \sqrt{ \dfrac{9225 - 432\sqrt{6} }{25} - \dfrac{28,8\sqrt{2550 - 288\sqrt{6} } }{5} } =$

$= \sqrt{ \dfrac{9225 - 432\sqrt{6} - 144\sqrt{2550 - 288\sqrt{6} }}{25} } = \dfrac{\sqrt{ 9225 - 432\sqrt{6} - 144\sqrt{2550 - 288\sqrt{6} } } }{5}$ $\approx 8,9$ .