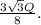Построение сводится к проведению перпендикуляра из точки к прямой.
Из вершины А, как из центра, раствором циркуля, равным АС, делаем насечку на стороне ВС. Обозначим эту точку К.
∆ КАС- равнобедренный с равными сторонами АК=АС.
Разделив КС пополам, получим точку М, в которой медиана ∆ КАС пересекается с основанием КС. Т.к. в равнобедренном треугольнике медиана=биссектриса=высота, отрезок АМ будет искомой высотой.
Для этого из точек К и С, как из центра, одним и тем же раствором циркуля ( больше половины КС) проведем две полуокружности. Соединим точки их пересечения с А.
Отрезок АМ разделил КС пополам и является искомой высотой ∆ АВС из вершины угла А.
Для прав. тр-ка центр описанной окр-ти лежит в точке пересеч. высот(медиан, биссектрис). Так как медианы в т. пересеч. делятся в отношении 2:1 считая от вершины, то радиус описанной окружности для прав. тр-ка равен 2/3 от медианы(высоты, биссектрисы). А так как высота прав. тр-ка равна (акор3)/2, то :
Построение сводится к проведению перпендикуляра из точки к прямой.
Из вершины А, как из центра, раствором циркуля, равным АС, делаем насечку на стороне ВС. Обозначим эту точку К.
∆ КАС- равнобедренный с равными сторонами АК=АС.
Разделив КС пополам, получим точку М, в которой медиана ∆ КАС пересекается с основанием КС. Т.к. в равнобедренном треугольнике медиана=биссектриса=высота, отрезок АМ будет искомой высотой.
Для этого из точек К и С, как из центра, одним и тем же раствором циркуля ( больше половины КС) проведем две полуокружности. Соединим точки их пересечения с А.
Отрезок АМ разделил КС пополам и является искомой высотой ∆ АВС из вершины угла А.
Сторона квадрата равна: корQ
Диагональ квадрата равна: корQ*кор2 = кор(2Q) и равна диаметру описанной окружности.
Значит радиус описанной окружности: R = кор(2Q) /2 = кор(Q/2) (1)
Для прав. тр-ка центр описанной окр-ти лежит в точке пересеч. высот(медиан, биссектрис). Так как медианы в т. пересеч. делятся в отношении 2:1 считая от вершины, то радиус описанной окружности для прав. тр-ка равен 2/3 от медианы(высоты, биссектрисы). А так как высота прав. тр-ка равна (акор3)/2, то :
R = (2/3)*(акор3)/2 = (акор3)/3 (2)
Приравняв (1) и (2), получим:
Площадь тр-ка:
S = (a^2кор3)/4 =