Classwork and homework Lesson 1 My favourite season Classicork 3a Work in pairs. Look, copy and complete. green play nice trees warm Winter Spring baby rainy animals green grass yard clean
1) Вначале рассмотрим тр-ки АВК и ДВМ. Они прямоугольные, т. к. ВК и ВМ - перпендикуляры по условию. АВ=ВС - у ромба все стороны равны между собой. Угол А = углу С - как противоположные углы ромба. Значит тр-ки равны по гипотенузе и острому углу. В равных тр-ках соответственные стороны равны, т. е. ВК=ВМ. АК=МС 2) Теперь рассмотрим тр-ки КВД и ДВМ. Они прямоугольные, ВД - общая сторона. ВК=ВМ из п. 1. Значит тр-ки равны по гипотенузе и катету. Отсюда КД=ДМ. А против равных сторон в равных тр-ках лежать равные углы, т. е. угол КВД=углуДВМ. Вывод ВД - луч, который разделил угол КВД на два равных угла, т. е. ВД-биссектриса, ч. т. д.
АВ=ВС - у ромба все стороны равны между собой.
Угол А = углу С - как противоположные углы ромба.
Значит тр-ки равны по гипотенузе и острому углу.
В равных тр-ках соответственные стороны равны, т. е. ВК=ВМ. АК=МС
2) Теперь рассмотрим тр-ки КВД и ДВМ.
Они прямоугольные, ВД - общая сторона.
ВК=ВМ из п. 1. Значит тр-ки равны по гипотенузе и катету.
Отсюда КД=ДМ. А против равных сторон в равных тр-ках лежать равные углы, т. е. угол КВД=углуДВМ. Вывод ВД - луч, который разделил угол КВД на два равных угла, т. е. ВД-биссектриса, ч. т. д.
Правильная треугольная пирамида - это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания.
Центр шара, вписанного в правильную пирамиду, лежит на её высоте.
Формула радиуса вписанной окружности для тетраэдра
По этой формуле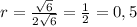
Подробное решение.(см. рисунок вложения)
Обозначим пирамиду SABC, SH - высота пирамиды, SM - апофема.
ОН и ОК - радиусы вписанного шара,
Проведем сечение пирамиды и шара плоскостью, проходящей через апофему и высоту пирамиды. При этом сечение шара будет вписанной в угол SМA окружностью.
∆ SHM прямоугольный. НМ - радиус окружности, вписанной в основание АВС пирамиды.
НМ=АМ:3 ( радиус вписанной в правильный треугольник окружности),
Так как тетраэдр правильный и, все его грани - правильные треугольники, их апофемы равны высоте правильного треугольника со стороной √6.
SM=AM=√6•√3/2=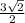
Радиус НМ вписанной в основание окружности равен AM/3=√2/2
КM=НM=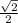
SK=SM-KM=3√2/2-√2/2=√2
∆SHM подобен ∆SKO ⇒
4r=2
r=0,5