Діагональ осьового перерізу циліндра дорівнює 8 см і утворює з площиною основи кут 30⁰. Знайдіть площу основи циліндра. а) 24п см^2 б)12п см^2 в)48п см^2 г)12п см^2

в нас є циліндр і осьовим перерізом є прямокутник , діогональ цього прямокутника дорівнює 8 см і кут з основою 30° з цього прямокутного трикутника , утвореного діагоналлюта сторанами перерізу , знаходимо , що висота циліндра - це катет , що лежить проти кута 30° і тому він дорівнює половині гіпотенузи ( діагоналі ) 4 см . З цього трикутника знаходиму другий катет за тиоремою піфагора - √48=4√3

отже радыус 2√3

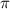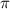площа основи = (2√3)² =12 см²

Г