Діагональ рівнобічної трапеції перпендикулярна до бічної сторони і утворюс з основою кут 30°. Знайти площу трапеції, якщо радіус її Описаного кола дорівнює 12 см.
Точка М является серединой боковой стороны АВ трапеции АВСД. Найдите площадь трапеции. если площадь. треугольника МСД равна 34. ------- Сделаем рисунок. Проведем МН параллельно основаниям трапеции. МН - средняя линия трапеции и делит СН пополам. МН - медиана треугольника СМД. Медиана треугольника делит его на два равновеликих. ⇒ S △ МСН=S △МДН=34:2=17 Продолжим прямую ВС за пределы трапеции. Через точку М проведем параллельно СД прямую до пересечения с прямой ВС в точке К, с АД - в точке Е. Тогда МКСН и МЕДН - равные параллелограммы - их противоположные стороны равны и параллельны. Диагональ параллелограмма делит его площадь пополам. Площадь МКС=площади МСН=17, а S КМНС=S МЕДН=17*2=34 В треугольниках МКВ и МАЕ имется две равные по условию стороны: АМ=МВ Углы при М равны как вертикальные, углы при В и А равны как накрестлежащие при параллельных прямых. Треугольник МКВ=треугольнику МАЕ по стороне и двум прилежащим к ней углам. Следовательно,S МКСН=S МВСН+S △ АМЕ, а S КСДЕ =S трапеции АВСД. S (АВСД=34*2=68 ( ед. площади)
Тело вращения представляет из себя цилиндр с высотой, равной меньшей стороне треугольника 13 см и радиусом оснований 16 см, из которого "вырезаны" усеченные конусы с равными радиусами и образующими 14 см и 15 см.
–––––––––––––––––––––––––––––––––––––––
Искомая площадь - сумма боковых поверхностей этих усеченных конусов S1+S2 и боковой поверхности цилиндра S3.
а) Для решения нужно найти радиус меньшей окружности, которая образуется при вращении вершины треугольника, противолежащей меньшей стороне.
Найдем высоту треугольника, проведенную к меньшей стороне, из его площади. Площадь треугольника со сторонами 13,14,15 встречается часто и равна 84 ( проверьте по ф.Герона)
-------
Сделаем рисунок.
Проведем МН параллельно основаниям трапеции.
МН - средняя линия трапеции и делит СН пополам.
МН - медиана треугольника СМД.
Медиана треугольника делит его на два равновеликих. ⇒
S △ МСН=S △МДН=34:2=17
Продолжим прямую ВС за пределы трапеции.
Через точку М проведем параллельно СД прямую до пересечения с прямой ВС в точке К, с АД - в точке Е.
Тогда МКСН и МЕДН - равные параллелограммы - их противоположные стороны равны и параллельны.
Диагональ параллелограмма делит его площадь пополам.
Площадь МКС=площади МСН=17, а
S КМНС=S МЕДН=17*2=34
В треугольниках МКВ и МАЕ имется две равные по условию стороны: АМ=МВ
Углы при М равны как вертикальные, углы при В и А равны как накрестлежащие при параллельных прямых.
Треугольник МКВ=треугольнику МАЕ по стороне и двум прилежащим к ней углам.
Следовательно,S МКСН=S МВСН+S △ АМЕ,
а S КСДЕ =S трапеции АВСД.
S (АВСД=34*2=68 ( ед. площади)
Тело вращения представляет из себя цилиндр с высотой, равной меньшей стороне треугольника 13 см и радиусом оснований 16 см, из которого "вырезаны" усеченные конусы с равными радиусами и образующими 14 см и 15 см.
–––––––––––––––––––––––––––––––––––––––
Искомая площадь - сумма боковых поверхностей этих усеченных конусов S1+S2 и боковой поверхности цилиндра S3.
а) Для решения нужно найти радиус меньшей окружности, которая образуется при вращении вершины треугольника, противолежащей меньшей стороне.
Найдем высоту треугольника, проведенную к меньшей стороне, из его площади. Площадь треугольника со сторонами 13,14,15 встречается часто и равна 84 ( проверьте по ф.Герона)
Высота равна 168:13=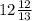 см
см
Радиус меньшей окружности равен R-h
Формула боковой поверхности усеченного конуса
Ѕ=πRL•(R+r)⇒
S1=π•14•(16+3,0769)=267,0766π см²
S2=π•15•(16+3,0769)=286,1535π см²
По формуле боковой поверхности цилиндра
S3=2πr•13=32•π•13=416π см²
S=969,2301π см² или ≈ 3044,926 см²