Дан параллелепипед abcda₁b₁c₁d₁. dc = 15 см, сс₁ = 8 см. точки m, n, k - середины сторон dc, cc₁ и b₁c₁ соответственно. выберите верные утверждения: а) mn коллинеарен вектору ав₁ б) mn коллинеарен вектору bk в) длина вектора mn равна 8,5 см г) вектор ab₁ равен вектору c₁d 1) а, в, г 2) а, б, в, г 3) а, в 4) а, б, в p.s с решением

Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 3см 4см. Найдите радиус круга, вписанного в треугольник​

Объяснение:

Пусть один катет а, другой катет b. . По т. о биссектрисе треугольника

, тогда а= .

По т. Пифагора а²+b²=(3+4)² 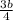 ,( )²+b²=49 ,

  +b²=49 ,    9b²+16b²=49*16  ,  b²= , b== 5,6 (см)

a=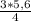   =4,2 cм

S=1/2*Р*r .   Найдем площадь прямоугольного треугольника

S=1/2*5,6*4,2=1/2*23,52 (см²) . Найдем периметр Р=16,8 см. Тогда

1/2*23,52=1/2*16,8*r , r= 23,52/16,8 , r=1,4 см

===============================

Теорема о биссектрисе треугольника " Биссектриса треугольника делит противоположную сторону на два отрезка, длины которых относятся так же, как длины соответствующих сторон."

Объяснение:

1)

Проведём две высоты ВК и CL

sin30°=BK/AB

BK=AB*sin30°=4*1/2=2

cos30°=AK/AB

AK=AB*cos30°=4*√3/2=2√3

АК=LD

BC=KL

AD=2*AK+KL=2*2√3+√3=5√3

S(ABCD)=BK(BC+AD)/2=2(√3+5√3)/2=6√3

ответ: площадь трапеции равна 6√3.

2)

∆LMO- прямоугольный, равнобедренный треугольник LO=MO

LO=LM/√2=6/√2=3√2/√2=3√2.

OB=MN

LK=2*LO+OB=2*3√2+2√2=8√2.

S(LMNK)=MO(MN+LK)/2=3√2(2√2+8√2)/2=

=3√2*10√2/2=15*2=30

ответ: площадь трапеции равна 30

3)

sin60°=BK/AB

BK=AB*sin60°=7*√3/2=3,5√3

cos60°=AK/AB

AK=AB*cos60°=7*1/2=3,5

AD=2*AK+BC=2*3,5+4=11

S(ABCD)=BK(BC+AD)/2=3,5√3(4+11)/2=

=3,5√3*15/2=26,25√3

ответ: площадь трапеции равна 26,25√3