Дано: abcd - четырёхугольник

угол 1=75 градусов

угол 2 не равен углу 4

угол 3 = 105 градусов

выяснить, является ли abcd - параллелограммом
(угол 5 уже дописала я, он там лишний это

Задание 3.  
коэффициент подобия k =a₁/a₂ >0 . 
(a₁/a₂)² =S₁/S₂ ⇒a₁=a₂*√(S₁/S₂) =9*√(75/300) =9*√(1/4) =9 /2 =4,5  (см).
Задание 4.
k = (a₁/a₂) =6 см / 4 см = 3/2 ;  S₁+S₂ =78 ;
{ S₁+S₂ =78 ;S₁/S₂ =(3/2)² . ⇔ { (S₁/S₂ +1)*S₂ =78 ;S₁/S₂ =9/4.  ⇔
{ (9/4 +1)*S₂ =78 ; S₁ =(9/4) *S₂.  ⇔ { (13/4)*S₂ =78 ;S₁ =(9/4)*S₂ ⇔                  { S₁ =(9/4)*24 ; S₂ =24 .⇔ { S₁ =54 (см²) ; S₂ =24 (см²).
Задание 5.
k =√ (S₁/S₂)  = √ (25/100)  =√ (1/4)  =1/2.
a₁/a₂ =k ⇔a₁ =k*a₂ =(1/2)*6 см =3 см и b₁ =k*b₂ =(1/2)*10  =5 см.
Задание 6.
Все  равносторонние  треугольники подобны 
 k² = (a₂/a₁)² = S₁/S₂ ⇒a₂ = a₁*√(S₁/S₂) =1* √ 3.
a₂ =√ 3..

площадь трапеции равна 63cos31° +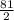 sin62° , что приблизительно равно 89.76

Объяснение:

Достроим рисунок высотами BE и CF.

Отметим, что площадь трапеции ABCD будет совпадать с площадью прямоугольника AFCG = AF*CF = (AE+EF)*BE = (7+AE)*BE

∠ABC=∠CBD=121° , ∠EBC=90°  значит ∠ABE=31°

В прямоугольном треугольнике ABE

sin∠ABE=AE/AB     ⇒ sin31°=AE/9       ⇒  AE=9*sin31°

cos∠ABE=BE/AB     ⇒ cos31°=BE/9       ⇒  BE=9*cos31°

Значит искомая площадь = (7+AE)*BE = (7+9*sin31°)*9*cos31° =

= 63cos31° + 81sin31°cos31° = 63cos31° +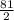 sin62° ≈ 89.76