Дано коло з центром в т.О. Січна перетинає його в точках А і В. Радіус кола дорівнює 8 см. Кут АОВ дорівнює 120 0 . Знайти відстань від центра кола до січної.
Вот на русском (могут быть ошибки) :
Даны окружность с центром в т.о. Секущая пересекает его в точках А и В. Радиус окружности равна 8 см. Угол АОВ равен 120. Найти расстояние от центра круга до секущей. ​​

Объяснение:

Задача №1.

Докажем равенство треугольников MKT и STP.

Для этого нам требуется три равных элемента.

1) KT = TP (по условию)

2) TM = ST (по условию)

3) ∠KTM = ∠PTS (вертикальные)

Следовательно, треугольники равны по двум сторонам и углу между ними.

Задача №2.

И опять же, нам требуются три равных элемента.

1) KN = KM (по условию)

2) PK - общая сторона обоих треугольников, то есть, это второй равный элемент.

3) Если меня не подводит мое зрение, то на чертеже указано, что угол NKP равен углу PKM (по условию), а из этого можно сделать вывод, что KP - биссектриса.

Следовательно, треугольники равны по двум сторонам и углу между ними.

Объяснение:

Задание №1.

Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.

Задание №2.

Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то этот треугольник - прямоугольный.

Задание №3.

Рассмотрим четыре равных прямоугольных треугольника.

Соединим эти четыре прямоугольных треугольника.

Получим квадрат, в который вписан еще один квадрат, похожий на ромб.

Одна половина стороны квадрата равна a, другая - b. Площадь первого квадрата будет равна (a+b)^2.

Сторона второго квадрата равна с, следовательно, площадь будет равна c^2.

А площадь всего многоугольника будет равна сумме площадей треугольников и второго квадрата.

Запишем это так:

4 * 0,5 * a * b + c^2 = a^2 + 2ab + b^2

Слева получим:

2ab + c^2 = a^2 + 2ab + b^2

2ab можем уничтожить.

Останется c^2 = a^2 + b^2

Теорема доказана.

А вот что такое "Приведите пример Пифагором треугольника" я не знаю.

4. Формула Герона для нахождения площади произвольного треугольника:

S =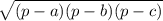

Где p - полупериметр треугольника, а все остальное - его стороны.