У произвольного треугольника есть формула площади :
, где h - высота, а - сторона, на которое падает основание высоты.
Прямоугольный же треугольник является частным случаем треугольника с тем отличием, что один из его углов равен 90 градусов. Тем не менее это не отменяет того факта, что для него работают все те же самые формулы, что и для обычного треугольника, поэтому площадь прямоугольного треугольника можно найти по нескольким формулам :
1. , где a и b - катеты (так как они пересекаются под углом в 90 градусов одного из них можно считать высотой)
2. , где c - гипотенуза, h - высота, опущенная на гипотенузу как на одно из оснований треугольника
Это задачи на применение теоремы Пифагора: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов, т.е.: с² = а² + b², где a и b - катеты, c - гипотенуза.
1. а = 9, b = 12, тогда с² = 9² + 12² = 81 + 144 = 225 = 15², откуда с = 15.
ответ: 15.
2. а = 12, с = b + 8. Найдем b и с.
По теореме Пифагора получим: 12² + b² = (b + 8)²,
144 + b² = b² + 16b + 64,
-16b = 64 - 144,
-16b = -80,
b = 5.
Тогда с² = 12² + 5² = 144 + 25 = 169 = 13², откуда с = 13.
ответ: 13.
3. с = 26, а = 10. Найдем S.
Из теоремы Пифагора найдем второй катет: b² = с² - а² = 26² - 10² =
= 676 - 100 = 576 = 24², откуда b = 24.
Площадь прямоугольного треугольника находят по формуле:
S = 1/2 · а · b, где а и b - катеты, S - его площадь.
У произвольного треугольника есть формула площади :
Прямоугольный же треугольник является частным случаем треугольника с тем отличием, что один из его углов равен 90 градусов. Тем не менее это не отменяет того факта, что для него работают все те же самые формулы, что и для обычного треугольника, поэтому площадь прямоугольного треугольника можно найти по нескольким формулам :
1.
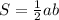, где a и b - катеты (так как они пересекаются под углом в 90 градусов одного из них можно считать высотой)
2.
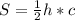, где c - гипотенуза, h - высота, опущенная на гипотенузу как на одно из оснований треугольника
Это задачи на применение теоремы Пифагора: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов, т.е.: с² = а² + b², где a и b - катеты, c - гипотенуза.
1. а = 9, b = 12, тогда с² = 9² + 12² = 81 + 144 = 225 = 15², откуда с = 15.
ответ: 15.
2. а = 12, с = b + 8. Найдем b и с.
По теореме Пифагора получим: 12² + b² = (b + 8)²,
144 + b² = b² + 16b + 64,
-16b = 64 - 144,
-16b = -80,
b = 5.
Тогда с² = 12² + 5² = 144 + 25 = 169 = 13², откуда с = 13.
ответ: 13.
3. с = 26, а = 10. Найдем S.
Из теоремы Пифагора найдем второй катет: b² = с² - а² = 26² - 10² =
= 676 - 100 = 576 = 24², откуда b = 24.
Площадь прямоугольного треугольника находят по формуле:
S = 1/2 · а · b, где а и b - катеты, S - его площадь.
Теперь S = 1/2 · 10 · 24 = 120.
ответ: 120.