Проведем отрезок BM, соединяющий вершину треугольника с точкой пересечения биссектрис. Биссектрисы треугольника пересекаются в одной точке, тогда отрезок BM является частью биссектрисы ∠B в ∆ABC, значит, ∠ABM = ∠CBM.
Так как AM – биссектриса ∠A, то ∠BAM = ∠MAC, тогда находим ∠A.
∠A = ∠BAM + ∠MAC = 30° + 30° = 60°.
Аналогично, так как CM – биссектриса ∠C, то ∠BCM = ∠ACM, тогда находим ∠С.
Проведем отрезок BM, соединяющий вершину треугольника с точкой пересечения биссектрис. Биссектрисы треугольника пересекаются в одной точке, тогда отрезок BM является частью биссектрисы ∠B в ∆ABC, значит, ∠ABM = ∠CBM.
Так как AM – биссектриса ∠A, то ∠BAM = ∠MAC, тогда находим ∠A.
∠A = ∠BAM + ∠MAC = 30° + 30° = 60°.
Аналогично, так как CM – биссектриса ∠C, то ∠BCM = ∠ACM, тогда находим ∠С.
∠С = ∠BCM + ∠ACM = 20° + 20° = 40°.
По теореме о сумме углов треугольника в ∆ABC:
∠A + ∠С + ∠B = 180°, следовательно ∠B = 180° – (∠A + ∠С) = 180° – (60° + 40°) = 180° – 100° = 80°.
Тогда находим ∠ABM.
∠ABM = 80° : 2 = 40°.
ответ: ∠ABM = 40°.
Формула вычисления стороны квадрата, зная описанный радиус: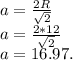
Формула вычисления радиуса вписанной окружности в квадрат, зная его сторону:
Вывод: Сторона квадрата равна: 16.97; радиус вписанной окружности — 8.5.
8.Формула вычисления радиуса описанной окружности, зная сторону правильного треугольника:
Длина круга равна:
Не поняла, площадь какого круга надо найти, так что найду площади и вписанной, и описанной окружности.
Формула вычисления площади описанной окружности такова:
Формула вычисления площади вписанной окружности такова: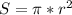
Радиус вписанной окружности в правильный треугольник, мы найдём по стороне этого же треугольника:
Площадь окружности равна:
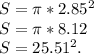
9.Формула вычисления стороны правильного треугольника, зная радиус описанной окружности:
Радиус вписанной окружности равен:
Площадь окружности равна: