Дано три точки А,В,С, які лежать на одній прямій. Скільки можна провести : а) площин через А,В,С; б) прямих, які проходять через точку В і паралельні прямій АС???

Показать ответ

Ответ:

мидина5

15.10.2020 14:16

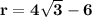ответ: $\bf r=4\sqrt3-6$ см .

ΔАВС - равнобедренный , АВ=ВС . ∠А=∠С=30° . R - радиус описанной окружности , r - радиус вписанной окружности , R=4 cм . Найти: r .

По теореме синусов имеем

$\dfrac{BC}{sinA}=2R\ \ \Rightarrow \ \ \ BC=2R\, sinA=2\cdot 4\cdot sin30^\circ =8\cdot \dfrac{1}{2}=4$ см .

Опустим перпендикуляр ВН из вершины В на основание АС . Точка Н будет серединой основания АС .

Найдём АН из ΔABH .

$cosA=\dfrac{AH}{AB}\ \ \ \Rightarrow \ \ \ AH=AB\cdot cosA=4\cdot cos30^\circ =4\cdot \dfrac{\sqrt3}{2}=2\sqrt3$ см

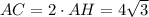Тогда $AC=2\cdot AH=4\sqrt3$ м .

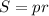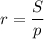Известна формула площади треугольника через радиус вписанной окружности : S=pr , где р - полупериметр . Отсюда можно выразить радиус вписан. окр-ти $r=\dfrac{S}{p}$ .

Найдём полупериметр ΔABС .

$p=\dfrac{1}{2}\cdot (AB+BC+AC)=\dfrac{1}{2}\cdot (4+4+4\sqrt3)=2\cdot (2+\sqrt3)=4+2\sqrt3$ см .

Теперь найдём площадь треугольника АВС .

$S=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA=\dfrac{1}{2}\cdot 4\cdot 4\sqrt3\cdot sin30^\circ =8\sqrt3\cdot \dfrac{1}{2}=4\sqrt3$ см²

$r=\dfrac{S}{p}=\dfrac{4\sqrt3}{2\cdot (2+\sqrt3)}=\dfrac{2\sqrt3\, (2-\sqrt3)}{(2+\sqrt3)(2-\sqrt3)}=\dfrac{2\sqrt3\, (2-\sqrt3)}{4-3}=4\sqrt3-6$ см

Кут при основі рівнобедреного трикутника дорівнює 30градусів. Радіус кола, описаного навколо трикутн

0,0(0 оценок)

Ответ:

светлана440

06.02.2021 07:40

Прямоугольник ABCD ⇒ ВС=AD=1 cм , CD=AB=√3 см .

АМ ⊥ плоскости ABCD ⇒ AM ⊥ АС , так как АМ ⊥ любой прямой, лежащей в плоскости ABCD . Значит , ΔАМС - прямоугольный и ∠МАС=90° ,

АМ=2 см .

Найдём длину АС из ΔACD , ∠ADC=90° как угол прямоугольника ABCD . По теореме Пифагора имеем

$AC^2=AD^2+CD^2\ \ ,\ \ AC^2=1^2+(\sqrt3)^2=1+3=4\ \ ,\ \ AC=\sqrt4=2$

Получили, что катеты прямоугольного ΔАМС равны по 2 см . Значит, этот треугольник равнобедренный . А так как он ещё и прямоугольный , то сумма острых углов равна 90° и ∠АМС=∠АСМ=90°:2=45° .

Угол между прямой АМ и плоскостью ABCD равен углу между наклонной АМ и её проекцией АС на эту плоскость .

Это будет угол ∠АСМ=45° .