Дано вектори а (4 -2 -4) та b (6 -3 2). Обчисліть (а - b)^2

5)точка O лежит на биссектрисе угла A так как точка O равноудалена от прямых AB и AC => ∠BAO=CAO=30°

∠OBA прямой => AO=2OB=5*2=10

AK=AO-KO=10-5=5

ответ 5

-----------------

6)AK=KC=3 так-как окружность лежит в точке пересечения биссектрис, а биссектриса равнобедренного треугольника опущенная к основанию является медианой и высотой поэтому радиус OK лежит на биссектрисе угла B и делит AC напополам.

AK=AM=3; KC=CN=3  и BN=BM=5 как отрезки касательных.

ответ 22

------------------

7)В прямоугольном треугольнике радиус вписанной окружности можно высчитать по формуле:

где p полупериметр,а (c) гипотенуза. (эта формула очень просто выводится из отрезков касательных, можешь сам попробовать ее вывести)

подставляем числа:

r=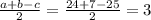

ответ: 3

28 + 4√97; 60°

Объяснение:

1. Пусть неизвестная сторона параллелограмма равна х см. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон, тогда:

12² + 32² = 28(14² + х²), откуда х² = 388. Тогда периметр параллелограмма равен 2*14 + 2√388 = 28 + 4√97.

2. Пусть острый угол между диагоналями параллелограмма равен α. Косинус острого угла между диагоналями параллелограмма равен отношению разности квадратов сторон параллелограмма к произведению его диагоналей, тогда:

cosα = (х² - 14²)/(12*32) = (388 - 196)/(12*32) = 1/2, и α = 60°