Дано: Векторы a и b - перпендикулярны
Вектор а = (1; 2; m+2)
Вектор b = (7; 2m-1; -3)
Найти:
m = ?

     Основанием пирамиды является прямоугольный треугольник с катетом а и прилегающим к нему острым углом α. Две боковые грани, содержащие катеты этого треугольника, перпендикулярны плоскости основания, а третья наклонена к ней под углом β. Найдите объем пирамиды.

  ========

Пусть в данной пирамиде АВС - основание. угол С=90°, ВС=а, ∠АВС=α, MC⊥(ABC) – высота пирамиды. Угол между АВС и АМВ=β.

Формула объёма пирамиды V=S•H:3

Угол МНС - линейный угол угла между плоскостями основания и грани АМВ и равен углу между перпендикулярами, проведенными к одной точке на АВ.

МН - наклонная, перпендикулярна АВ, СН - её проекция на АВС.⇒ По т. о 3-х перпендикулярах угол СНВ=90°, а СН - высота ∆ АВС

S=a•b•sinα:2 ⇒

S(АВС)=AB•BC•sinα:2

АВ=ВС:cosα=a:cosα

S(АВС)=(a:cosα)•a•sinα:2=a²sinα:2cosα

H=MC=CH•tgβ

CH=BC•sinα=a•sinα

H=a•sinα•tgβ

V=(a²•sinα:2cosα)•a•sinα•tgβ:3⇒

ответ: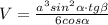

:

Две сферы.

V = 500п/3 ед. кб.

d = 10 ед.

V - ?

R1 - радиус первой сферы.

R2 - радиус второй сферы.

Составим уравнение, с которого узнаем, чему равен радиус R1

Пусть х - радиус R1

V сферы = 4/3пR^3 = 500п/3

В уравнении число п нам не нужно, так как при вычислении объёма сферы, видео, что число п не вычислялось:

4/3 * х^3 = 500/3

х^3 = 125

х^3 = 5^3

х = 5

Итак, R = 5 см

Так как d = 10 см => R1 = R2 = 5 см, так как R1 + R2 = 5 + 5 = 10 см

Из этого =>, что две сферы касаются внешним образом.

=> сферы образуют одну общую точку, но они не образуют никакой фигуры, то есть V = 0