Углы, прилежащие к боковой стороне трапеции в сумме равны 180°.
⇒ ∠В = 180° - 60° = 120°
∠D = 180° - 120° = 60°
Если углы при основаниях трапеции равны, то трапеция - равнобедренная.
⇒ АВ = CD
2. Рассмотрим ΔАВН - прямоугольный.
В равнобедренной трапеции высота, опущенная из вершины тупого угла на большее основание, делит его на части, меньшее из которых равна полуразности оснований.
⇒
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠1 = 90° - 60° = 30°
Катет, лежащий против угла в 30°, равен половине гипотенузы.
Построим Высоту BH. Из-за того, что это высота, ∠HBC = 90°,⇒(Следовательно) ∠ABH = 135° - 90° = 45°. Т.к ∠AHB = 90° (Смежный с Прямым углом), и в этом Δ-ке есть ∠-ол 45°, то ΔAHB - равнобедренный (По свойству прямоугольного Δ-ка).
Пусть х = AH = BH. Тогда 2x² = (3√2)².
Составим уравнение:
2x² = (3√2)²
2x² = 9×2 |÷2
x² = 9
√x² = √9
x = 3.
Таким образом получили, что AH = BH = 3, а так как BH - высота, то используем формулу площади, так как есть все нужные данные:
АВ = CD = 2
Объяснение:
Дано: ABCD - трапеция.
∠А = 60°; ∠С = 120°;
ВС = 3; AD = 5.
Найти: АВ и CD.
ВН - высота.
1. Рассмотрим ABCD.
Углы, прилежащие к боковой стороне трапеции в сумме равны 180°.⇒ ∠В = 180° - 60° = 120°
∠D = 180° - 120° = 60°
Если углы при основаниях трапеции равны, то трапеция - равнобедренная.⇒ АВ = CD
2. Рассмотрим ΔАВН - прямоугольный.
В равнобедренной трапеции высота, опущенная из вершины тупого угла на большее основание, делит его на части, меньшее из которых равна полуразности оснований.⇒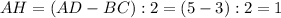
Сумма острых углов прямоугольного треугольника равна 90°.⇒ ∠1 = 90° - 60° = 30°
Катет, лежащий против угла в 30°, равен половине гипотенузы.⇒ AB = AН ·2 = 1 · 2 = 2
АВ = CD = 2
24
Объяснение:
Построим трапецию ABCD.
Построим Высоту BH. Из-за того, что это высота, ∠HBC = 90°,⇒(Следовательно) ∠ABH = 135° - 90° = 45°. Т.к ∠AHB = 90° (Смежный с Прямым углом), и в этом Δ-ке есть ∠-ол 45°, то ΔAHB - равнобедренный (По свойству прямоугольного Δ-ка).
Пусть х = AH = BH. Тогда 2x² = (3√2)².
Составим уравнение:
2x² = (3√2)²
2x² = 9×2 |÷2
x² = 9
√x² = √9
x = 3.
Таким образом получили, что AH = BH = 3, а так как BH - высота, то используем формулу площади, так как есть все нужные данные:
(a + b)/2 × h = (6+10)/2 × 3 = 8×3 = 24