Даны координаты векторов a→ и b→. Определи координаты векторов a→+b→ и b→−a→.

a→{7;7};

b→{−27;−10};

a→+b→{
;
};

b→−a→{
;
}.

Определи длину данных векторов, если известны их координаты.
(Если это необходимо, ответ округли до десятых.)
a→{3;−4} ∣∣a→∣∣=
;

b→{−4;3} ∣∣∣b→∣∣∣=
;

c→{−6;8} ∣∣c→∣∣=
;

d→{8;−6} ∣∣∣d→∣∣∣=
.

Даны точки V(4;4) и N(−9;7) . Найди координаты вектора VN−→ и вектора NV−→.

VN−→ {
;
};

NV−→ {
;
}.

Каковы эти векторы? Выбери правильные варианты ответа.

Сонаправленные
Равные по длине
Равные
Противоположно направленные

Даны координаты векторов a→ и b→.
Определи координаты векторов u→ и v→, если u→=3a→−2b→ и v→=2a→+b→.

a→{1;5};

b→{7;5}.

u→{
;
};

v→{
;
}.

Даны векторы VN−→{−3;1} и MT−→−{−6;4}.
Вычисли: 5⋅VN−→−4⋅MT−→−.

ответ:{
;
}.

Даны векторы VN−→{−8;2} и MT−→−{1;9}.

Вычисли:

VN−→+MT−→− = {
;
};

VN−→−MT−→− = {
;
};

7⋅VN−→ = {
;
}.

Найди периметр треугольника ABC, если его вершины имеют следующие координаты: A(2;2), B(5;7) и C(3;9).

P=
−−−−−−√+
−−−−−−√.

16; 16; 16. Цей рівнобедрений трикутник є рівностороннім

Объяснение:

Площа трикутника дорівнює ½ah. Знайдемо висоту. Вона ділить основу на дві рівні частини. Розглянемо один з отриманих прямокутних трикутників. У ньому гострий кут 30°. Знаємо, що tg30°=√3/3. Отже, висота поділена на половину основи попереднього рівнобедреного трикутника складає √3/3. Знаємо ще те, що Ця ж висота помножена на цю ж половину основи складає 64√3 см². Отже, ми отримали таку систему:(нехай половина основи = х, а висота - у)

х/у=√3/3;

ху=64√3

Є таке ноу-хау: метод множення:

х×х×у÷у=64√3×√3/3

х²=(64×√3×√3)/3

х²=64

х=√64=8

Підставимо х у рівняння ху=64√3

у=64√3/8=8√3

Тепер повернемося до прямокутного трикутника.

х=8, у=8

Знайдемо гіпотенузу (це бокова сторона рівнобедреного трикутника) Нехай вона дорівнює с.

За теоремою Піфагора, с²=х²+у²

с²=64+(8√3)²=64+64×3=256

с=√256=16

Тепер залишилось знайти основу. Ми знаємо, що х - це половина основи, тобто основа дорівнює 2х.

2х = 2×8=16

12 см

Объяснение:

есть одно интересное свойство:

медиана прямоугольного треугольника есть радиусом описанной вокруг этого треугольника окружности, а диаметр такой окружности раден гипотенузе (это можно доказать из свойств угла, расположеного в окружности (прямой вписанный угол опирается на диаметр окружности) или как следствие теоремы, что центр описанной окружности вокруг прямоугольного треугольника лежит на середине гипотенузы)

Значит длина гипотенузы = 2*СD = 5 cm

один из катетов = 5-1 = 4 см

второй катет =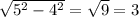 cм

P = 5+4+3 = 12 см