Площадь правильного треугольника находится по формуле
,
где a - длина стороны треугольника
Площадь любой из граней пирамиды равна
или
1)
Площадь боковой поверхности равна сумме трех площадей правильного треугольника со стороной 11 см.
3)
4) Площадь полной поверхности равна сумме четырех площадей правильного треугольника со стороной 11 см.
или
2) Объем найти сложнее. Нужна высота пирамиды.
Высоту можно найти из прямоугольного треугольника, образованного высотой пирамиды (это катет), Стороной (боковой гранью) пирамиды (гипотенуза) и частью высоты треугольника, лежащего в основании пирамиды (второй катет). Такой треугольник будет прямоугольным, так как высота перпендикулярна всей плоскости основания пирамиды (в том числе и отрезку, соединеящему основание высоты и боковую грань-как раз второй катет.). Нам нужно найти второй катет. Высота пирамиды падает на центр и вписанной и описанной окружности. Так как пирамида правильная. Это будет пересечение биссектрис или серединных перпендикуляров. В правильном треугольнике точка пересечения биссектрис совпадает с точкой пересечения медиан. А медианы в точке пересечения делятся в отношении 2 к 1 считая от вершины. Значит длина второго катета равна 2/3 высоты правильного треугольника со стороной 11 см. Высота правильного треугольника равна по формуле
В данном случае
2/3 от этой высоты равна
По теореме Пифагора найдем первый катет в прямоугольном треугольнике
Дана правильная треугольная пирамида
со стороной основания 14 и боковым ребром 26.
Найти:
площадь боковой поверхности
площадь полной поверхности
объем.
---------------------
Площадь боковой поверхности пирамиды состоит из площади трех граней - равнобедренных треугольников с основанием 14 и боковыми сторонами 26.
Sтр-ка=аh:2
Высоту h такого треугольника найдем по т. Пифагора из его половиы -
прямоуголього треугольника АМК.
МК=√(АМ²-АК²)
МК=√(26²-7²)=√(676-49)=√627
S грани=МК·АС:2=7√627 ≈175.27977 ≈175,28
Sбок=3·7√627 =21√627
или ≈525,84
Полная поверхость пирамиды - сумма площади боковой поверхности и площади основания.
Площадь основания найдем по формуле:
Sосн=(a²√3):4
Sосн=(14²√3):4=196√3):4=49√3 ≈84,87
Sполн= 21√627+49√3=7√3(3√209+7)
или ≈ 525,84+84,87= ≈610,71
Объем пирамиды равен одной трети произведения площади основания на высоту.
Высоту трапеции следует найти.
Для этого рассмотрим треугольник АОМ.
АО- отрезок высоты, равный радиусу окружности, описанной вокруг правильного треугольника АВС, и равен он 2/3 высоты АЕ треугольника АВС.
АЕ по формуле высоты правильного треугольника
АЕ=(а√3):2=14√3):2=7√3
МО=√АМ²-АО²)
МО=√{(26²-(7√3)²}=√ 529=23
V=(23·49√3):3= 1127√3):3
или ≈650,67
-----------------
Нельзя сказать. что результат вычислений привычен, но из этих величин получается именно так.
Проверено несколько раз
Площадь правильного треугольника находится по формуле
где a - длина стороны треугольника
Площадь любой из граней пирамиды равна
или
1)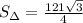
Площадь боковой поверхности равна сумме трех площадей правильного треугольника со стороной 11 см.
3)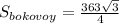
4) Площадь полной поверхности равна сумме четырех площадей правильного треугольника со стороной 11 см.
или
2) Объем найти сложнее. Нужна высота пирамиды.
Высоту можно найти из прямоугольного треугольника, образованного высотой пирамиды (это катет), Стороной (боковой гранью) пирамиды (гипотенуза) и частью высоты треугольника, лежащего в основании пирамиды (второй катет). Такой треугольник будет прямоугольным, так как высота перпендикулярна всей плоскости основания пирамиды (в том числе и отрезку, соединеящему основание высоты и боковую грань-как раз второй катет.). Нам нужно найти второй катет. Высота пирамиды падает на центр и вписанной и описанной окружности. Так как пирамида правильная. Это будет пересечение биссектрис или серединных перпендикуляров. В правильном треугольнике точка пересечения биссектрис совпадает с точкой пересечения медиан. А медианы в точке пересечения делятся в отношении 2 к 1 считая от вершины. Значит длина второго катета равна 2/3 высоты правильного треугольника со стороной 11 см. Высота правильного треугольника равна по формуле
В данном случае
2/3 от этой высоты равна
По теореме Пифагора найдем первый катет в прямоугольном треугольнике
Объем пирамиды находим по известной формуле