1. Отложим от точки B отрезок BE такой, что он лежит на прямой, параллельной AC, а точка E лежит на прямой AD (то есть выполним параллельный перенос отрезка AC на вектор CB). Поскольку EA || BC как прямые, содержащие основания трапеции, а AC || BE по построению, то AEBC — параллелограмм, откуда BC = EA. Поскольку углы ∠AOD и ∠EBD соответственные при параллельных прямых AC и EB, то они равны, а значит, EB ⊥ BD. Но BA ⊥ ED по условию, значит, в прямоугольном ΔEBD BA — высота, опущенная из прямого угла. Тогда .
2. В прямоугольном ΔABD . В прямоугольном ΔABC . AO — высота, опущенная из прямого угла, . Аналогично .
ответ:Дан ромб, сторона которого равна 17 см, а разность диагоналей - 14 см.
Диагонали d1 и d2 ромба перпендикулярны, образуют 4 треугольника.
По заданию d1 - d2 = 14. Разделим на 2 обе части.
(d1/2) - (d2/2) = 7.
Обозначим (d1/2) за х - это катет треугольника.
Второй катет равен х - 7.
По Пифагору a ² = (d1/2) ² + (d2/2) ².
289 = x² + (x - 7) ².
289 = x² + x² - 14x + 49.
2x² - 14x = 240 разделим на 2 и получаем квадратное уравнение.
х² - 7 х - 120 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D = (-7) ^2-4*1 * (-120) = 49-4 * (-120) = 49 - (-4*120) = 49 - (-480) = 49+480=529;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1 = (√529 - (-7)) / (2*1) = (23 - (-7)) / 2 = (23+7) / 2=30/2=15;
x_2 = (-√529 - (-7)) / (2*1) = (-23 - (-7)) / 2 = (-23+7) / 2=-16/2=-8.
Один катет получен: (d1/2) = 15 см, второй равен 15 - 7 = 8 см.
Площадь ромба равна:
S = 4 * (1/2) * 15*8 = 15*16 = 240 см².
Объяснение:
1.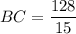
2.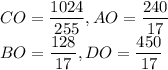
Объяснение:
1. Отложим от точки B отрезок BE такой, что он лежит на прямой, параллельной AC, а точка E лежит на прямой AD (то есть выполним параллельный перенос отрезка AC на вектор CB). Поскольку EA || BC как прямые, содержащие основания трапеции, а AC || BE по построению, то AEBC — параллелограмм, откуда BC = EA. Поскольку углы ∠AOD и ∠EBD соответственные при параллельных прямых AC и EB, то они равны, а значит, EB ⊥ BD. Но BA ⊥ ED по условию, значит, в прямоугольном ΔEBD BA — высота, опущенная из прямого угла. Тогда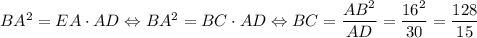 .
.
2. В прямоугольном ΔABD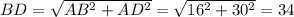 . В прямоугольном ΔABC
. В прямоугольном ΔABC 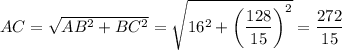 . AO — высота, опущенная из прямого угла,
. AO — высота, опущенная из прямого угла, 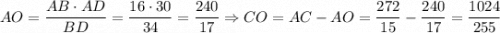 . Аналогично
. Аналогично 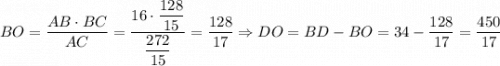 .
.