Даны уравнения двух прямых: -2х-7у+1=0 и 3х+4у+5=0
Найдите координаты (х0; у0) точки пересечения этих прямых. в ответе запишите сумму х0+у0
а) -2 б) 2 в) -1 г) 1

Описанный четырехугольник — это четырехугольник, все стороны которого касаются окружности. При этом окружность называется вписанной в четырехугольник. Какими свойствами обладает вписанная в четырехугольник окружность? Когда в четырехугольник можно вписать окружность? Где находится центр вписанной окружности? Теорема 1. ... В четырехугольник ABCD можно вписать окружность, если. Ab+CD=bc+ad. И обратно, если суммы противоположных сторон четырехугольника равны: Ab+CD=bc+ad ... Центр вписанной в четырехугольник окружности — точка пересечения его биссектрис. O — точка пересечения биссектрис четырехугольника ABCD. AO, BO, CO, DO — биссектрисы углов четырехугольника ABCD, то есть ∠BAO=∠DAO, ∠ABO=∠CBO и т.д.

Рисунок прилагается. Таких внешних касательных существует всего две. Они пересекаются в точке G. BD и CF - радиусы, перпендикулярные касательной GE. Треугольники GDB и GFC подобны по двум углам (G - общий угол, а также ∠GBD=∠GFC=90° (как раз эти самые радиусы)

Тогда из подобия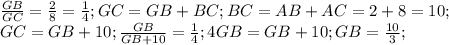

Наше искомое расстояние AP. Это заодно значит, что AP перпендикулярно GT (второй касательной, можно было так же начертить и с первой, это не принципиально). Тогда треугольники GBH и GAP тоже подобны по двум углам (G - общий и ∠GHB=∠GPA=90°)

и значит, что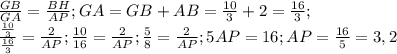

ответ: 3,2 см.