ДАЮ 20б
Производные основных элементарных функций
Производные основных элементарных функций представлены в таблице в предыдущей теме (см. файл Производная функции). Рассмотрим примеры
1) Y=4*sinx, Y’=4*cosx
2) Y=ex+5x, y’=ex+5
3) Y=sinx*cosx, используем правило производной произведения двух функций:
y’=(sinx)’*cosx+sinx*(cosx)’=cos2x-sin2x
4) Y=sinx/(2x), применяем правило производной частного двух функций:
y’=((sinx)’*2x-sinx*(2x)’)/(4x2)=(2x*cosx-2*sinx)/(8x)
Производная сложной функции
Сложная функция- если y=f(u), а u=g(x). Производная сложной функции вычисляется по следующему правилу Y’= f ’(U) * U’
Примеры:
1) Y=(x2+1)3=U3, где U=x2+1
Y’=( U3)’ * (x2+1)’=3U2*2x=3(x2+1)2*2x
2) Y=sin(2x+5)=sin(U), где U=2x+5
Y’=(sinU)’ * (2x+5)’= cosU*2=2cos(2x+5)
Т.е. когда производная f ’(U) найдена, вместо U подставляют ее выражение
Производная высших порядков
Производную функции можно брать несколько раз, поэтому говорят не только о первой, но и о второй, третьей и т.д. производных. Пример:
Y=x4, Y’=4x3, Y’’=12x2, Y’’’=24x
Производная высших порядков
Производную функции можно брать несколько раз, поэтому говорят не только о первой, но и о второй, третьей и т.д. производных. Пример:
Y=x4, Y’=4x3, Y’’=12x2, Y’’’=24x
Задачи:
1) Найти первую, вторую и третью производную функции y=1/x
2) Найти производную следующих функций:
a. Y= ex * 5x (произведение двух функций)
b. Y= e2x+1 (сложная функция)
c. Y= ln(x2-1) (сложная функция)
d. Y= 4cosx+2sinx (сумма двух функций)
e. Y= (x2+3x+1)2 (сложная функция)
f. Y= tg(3x+5) (сложная функция)
Применение производной к исследованию функций и построению графиков
Исследовать функции на монотонность и экстремумы:
1) y=3x/(1+x2)
2) y=x3/3 – 5x2/2 + 6x
3) y=2x-x3/6
Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство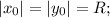 учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти)
учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти) 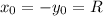
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
и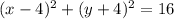
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
k_1k_2=-1
поєтому угловой коєффициент искомой пряммой равен k=-1/(-0.5)=2
учитывая что искомая пряммая проходит через точку С ищем ее уравнение в виде
y=kx+b (k=2)
2=2*0+b;
b=2
y=2x+2 или y-2x-2=0
в чем ошибка у вас - неведомо, ибо вы своего решения не предоставили
Площадь параллелограмма равна произведение основания на высоту. Нам дана площадь и сторона параллелограмма, значит высота равна 187/17=11 см
№2
Высота = 18/3=6 см
Формула площади: половина произведения основания на высоту, значит площадь равна 1/2 *18*6=54 см
№3
Высота = 1/2 * (4+12)=8 см
Форумла площади трапеции: произведение полусуммы оснований на высоту, значит площадь равна 1/2 (4+12) * 8 =64 см
№4
Острый угол параллелограмма равен 180-150=30 градусов (т.к. односторонний при параллельных прямых). Проведем высоту, получился прямоугольных треугольник с гипотенузой 4 см и острым углом в 30 гарудсов, значит по свойству прямоугольного треугольника высота равна 1/2 * 4=2 см. Площадь равна 7*2=14см
№5
Обозначим одну часть за х. Тогда 3х+5х=8, значит х=1. значит диагонали ромба равны 3см и 5 см
Формула площадь : половина произведения диагоналей
Найдем площадь 1/2 * 3 * 5 = 7,5 см