Так как любой внутренний угол квадрата равен 90 градусам. Диагональ квадрата проходит от противолежащих его углов друг к другу и делит квадрат на два равных треугольника. Треугольники получаются прямоугольными и равнобедренными Возьмем прямоугольно-равнобедренный треугольник и просчитаем градусы углов треугольника. Их сумма равна 180 градусов. Прямой угол треугольника равен 90 градусов. Из суммы углов треугольника вычитаем этот угол и останется 90 градусов на два других угла. Треугольник равнобедренный, => два оставшихся угла равны. Делим 90 градусов на 2 и получаем по 45 градусов каждый угол. Когда эти два треугольника "склеиваются" гипотенузами, получается квадрат. Гипотенуза любого из "склеившихся" треугольников становится диагональю этого квадрата. Углы по 45 градусов с одной стороны диагонали и с другой сложились и получились прямые углы квадрата, равные 90 градусам . А как сказано выше, в любом квадрате каждый внутренний его угол равен 90 градусов. А этой ситуации диагональ делит два противолежащих угла пополам, она будет являться его биссектрисой
Объяснение:
Так как любой внутренний угол квадрата равен 90 градусам. Диагональ квадрата проходит от противолежащих его углов друг к другу и делит квадрат на два равных треугольника. Треугольники получаются прямоугольными и равнобедренными Возьмем прямоугольно-равнобедренный треугольник и просчитаем градусы углов треугольника. Их сумма равна 180 градусов. Прямой угол треугольника равен 90 градусов. Из суммы углов треугольника вычитаем этот угол и останется 90 градусов на два других угла. Треугольник равнобедренный, => два оставшихся угла равны. Делим 90 градусов на 2 и получаем по 45 градусов каждый угол. Когда эти два треугольника "склеиваются" гипотенузами, получается квадрат. Гипотенуза любого из "склеившихся" треугольников становится диагональю этого квадрата. Углы по 45 градусов с одной стороны диагонали и с другой сложились и получились прямые углы квадрата, равные 90 градусам . А как сказано выше, в любом квадрате каждый внутренний его угол равен 90 градусов. А этой ситуации диагональ делит два противолежащих угла пополам, она будет являться его биссектрисой
Объяснение:
1. A(0;0) B(9;10).
Уравнение прямой:
ответ: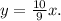
2. A(0;0) B(5;0) C(12;-3) Dₓ=?
ответ: Dₓ=7.
3. M(2;-4) K(3,5) P(x;y)=?
ответ: P(-1;-31).
4.
(x-3)²+(y-5)²=49
(x-3)²+(y-5)²=7²
Графиком этого уравнения является окружность, центр которой смещён вправо вдоль оси Ох на 3 единицы и опущен вниз вдоль
оси Оу на 5 единиц с радиусом 7 единиц.
Рассиояние от центра окружности (x-3)²+(y-5)²=7² до прямой х=-2
равно: 3-(-2)=3+2=5<R(7) ⇒ Прямая пересекает окружность в двух точках.
5. Рассмотрим ΔАКО. АК=КО=АО*tg∠АОК=8*√2*√2/2=8 (cм).
Рассмотрим ΔВСО. ОС=√(ОВ²-ВС²)=√(10²-8²)=√(100-64)=√36=6 (см).
Продлим прямые АК и ВС до точки пересечения F. ⇒
AF=8+6=14 (см) BF=4528+8=16 (см).
AB=√(AF²+BF²)=√(14²+16²)=√(196+256)=√452=2√113≈21,26 (см).
A(-8;-8) B(8;-6).