Площадь полной поверхности пирамиды (обозначим её МАВСD) состоит из суммы площадей всех граней. Противоположные боковые грани равны по трём сторонам. Так как МО перпендикулярна плоскости основания, а ВD⊥АВ и CD, то ОВ – проекция наклонной МВ. По т.о 3-х перпендикулярах МВ⊥АВ.Диагонали параллелограмма точкой пересечения делятся пополам ⇒. ОВ=1,5.Высота пирамиды МО⊥ОВ. Из ∆ МОВ по т.Пифагора МВ=√(МО²+ОВ²)=√(4+2,25)=2,5Ѕ(АМВ)=МВ•АВ:2=2,5•4:2=5 м²Ѕ(MCD)=S(AMB) ⇒Ѕ(MCD)+S(AMB)=10 м²Найдём высоту второй пары боковых граней. а) Высота DHпрямоугольного ∆ BDH (в основании) равна произведению катетов, делённому на гипотенузу. DH=DB•DC:BC=3•4:5=2,4 мПроведем ОК⊥ВСВO=ОD ⇒ ОК - средняя линия ∆ВDH и равна половине DH.ОК=1,2 мОК - проекция наклонной МК. ⇒ По т.ТПП отрезок МК⊥ВС и является высотой ∆ ВМСб) Из прямоугольного ∆ МОК по т.Пифагора МК=√(MO²+OK²)=√(4+1,44)=√5,44√5,44=√(544/100)=(2√34):10=0,2√34 S(MBC)=BC•MK:2=0,5•5•0,2√34=0,5√34 м² S(AMD)=S(MBC)⇒ S(AMD)+S(MBC)=2•0,5√34=√34 м²S(ABCD)=DB•AB=3•4=12 м²Площадь полной поверхности MABCD:2•S(AMB)+S(ABCD)+2•S(MBC=10+12+√34=(22+√34)м²
A)По т.Менелая
(СД:ДА)•(АЕ:ЕК)•(ВК:ВС)=1
(
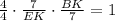, откуда получим ВК:ЕК=1, следовательно, ВК=ЕК.
2)Проверим ∆ АВС по т.Пифагора.
AB² > АС²+ВС² => угол С тупой.
По ф.Герона S(ABC)-√(14•7•6•1)=14√3
ВD- медиана и делит треугольник на два равных по площади.
S(BCD)=7√3
По другой формуле
S (ABC)=AC•BC•sinC:2
14√3=8•7•sinC:2 => sinC=√3/2 => тупой угол С=120°
(Можно подтвердить по т.косинусов – получим cos C= -1/2)
Из вершины А проведем высоту АН.
Высота тупоугольного треугольника, проведенная из острого угла, находится вне треугольника и пересекается с продолжением стороны, к которой проведена.
Угол АСН =180°-120°=60°( смежный углу АСВ)
НС=АС•cos60°=4
AH=AC•sin60°=4√3
Примем ВК=ЕК=х
В ∆ АНК
АК=АЕ+ЕК=7+х
КС=ВС-ВК=7-х
АК²=АН²+КН² =(7+х)²=(4√3)²+(4+7-х)²
49+14х+х²=121-22х+х²+48=>
ВК=х=10/3
СК=7-10/3=11/3
AK=7+10/3=31/3
Площадь DЕКС найдем из разности площадей ∆ АСК и ∆ АЕD.
S(AKC)=AH•CK:2=(4√3•11/3):2=22/√3 =>
sinCAK=22/√3:(8•31/6)=11√3/62
S(AED)=AD•AE•sinA:2=77√3/31
S(CDEK)=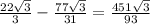
(ед. площади)