До іть будьласка з геометріей (2 завдання)​

дано: δ авс

∠с = 90°

ак - биссектр.

ак = 18 см

км = 9 см

найти:   ∠акв

решение.

      т.к. расстояние от точки  измеряется по перпендикуляру, то опустим его из (·) к  на гипотенузу ав и обозначим это расстояние км.

      рассмотрим полученный δ акм, т.к.  ∠амк = 90°,то ак гипотенуза, а км - катет. поскольку, исходя из  условия, катет км = 9/18 = 1/2 ак, то  ∠кам = 30°. 

      т.к. по условию ак - биссектриса, то  ∠сак =∠кам = 30°

      рассмотрим  δакс. по условию  ∠аск = 90°; а∠сак = 30°, значит,  ∠акс = 180° - 90° - 30° = 60°

      искомый  ∠акв - смежный с  ∠акс, значит,  ∠акв = 180° - ∠акс = 180° - 60° = 120° 

ответ: 120°

Здравствуйте, Jdirjmnab!

Решим данную задачу алгебраическим через уравнение).

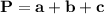
Пусть x (см) равна боковая сторона, тогда основание будет равно (x-14) (см). Т.к. боковые стороны равнобедренного тр-ка равны, то вторая боковая сторона тоже x (см). Периметр тр-ка равен 76 (см).

I этап. Составление математической модели:

II этап. Работа с математической моделью:

III этап. ответ математической модели:

(см) равна боковая сторона.

IV этап. ответ на вопрос задачи:

Т.к. боковые стороны равны, то их сумма равна 30+30=60 (см).

Тогда основание равно: 76-60=16 (см) или 30-14=16 (см).

По правилу сумма двух сторон тр-ка должна быть больше одной стороны.

30+30>16 - верно;       30+16>30 - верно;       30+16>30 - верно.

В данном тр-ке: "боковые стороны по 30 (см), основание 16 (см).

С Уважением, NeNs07.