Доказать, что при пересечении двух параллельных прямых секущей. а) соответственные углы равны б) сумма односторонних равны 180°​

Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности ({\displaystyle R=t}R=t), поскольку {\displaystyle 2\sin {\frac {\pi }{6}}=1}2\sin {\frac {\pi }{6}}=1.

Все углы равны 120°.

Радиус вписанной окружности равен:

{\displaystyle r={\frac {\sqrt {3}}{2}}R={\frac {\sqrt {3}}{2}}t}r={\frac {{\sqrt 3}}{2}}R={\frac {{\sqrt 3}}{2}}t

Периметр правильного шестиугольника равен:

{\displaystyle P=6R=4{\sqrt {3}}r}P=6R=4{\sqrt 3}r

Площадь правильного шестиугольника рассчитывается по формулам:

{\displaystyle S={\frac {3{\sqrt {3}}}{2}}R^{2}={\frac {3{\sqrt {3}}}{2}}t^{2}}S={\frac {3{\sqrt 3}}{2}}R^{2}={\frac {3{\sqrt 3}}{2}}t^{2}

{\displaystyle S=2{\sqrt {3}}r^{2}}S=2{\sqrt 3}r^{2}

Шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).

Правильный шестиугольник со стороной {\displaystyle {\frac {1}{\sqrt {3{\frac {1}{{\sqrt 3}}} является универсальной покрышкой, то есть всякое множество диаметра 1 можно покрыть правильным шестиугольником со стороной

Точка S находится на одном расстоянии от всех вершин правильного треугольника со стороной 2 корня из 3 см и відалена от плоскости треугольника на корень из 3 см найдите расстояние от точки S до вершины треугольника.

Объяснение:

Т.к. точка S находится на одном расстоянии от всех вершин правильного треугольника, то SA=SB=SC.

Расстояние от  S  до плоскости ( АВС) √3 см⇒SO⊥(АВС). Тогда прямоугольные треугольники равны по катету (SO-общий) и гипотенузе ( SA=SB=SC.)  ΔSOA=ΔSOB=ΔSOC ⇒ОА=ОВ=ОС и значит О-центр описанной окружности около правильного ΔАВС и ОА=ОВ=ОС=R =  ,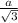

R =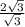 =2 (см)

ΔSOA- прямоугольный , по т. Пифагора SA= √(2²+√3²)=√7 (cм)