В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)= =9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
=√3 см
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
=√147 см
Боковые грани правильной пирамиды это равные треугольники.
В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)=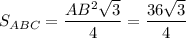 =9√3 см².
=9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
Боковые грани правильной пирамиды это равные треугольники.
S(бок.)=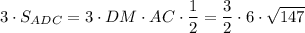 =9√147 см²
=9√147 см²
S(полн.) = S(осн.)+S(бок.) = 9√3 + 9√147 см²
ответ: 9√3 + 9√147 см².
АВ = √((Хв-Ха)²+(Ув-Уа)²) = √40 = 6.32455532,
BC = √((Хc-Хв)²+(Ус-Ув)²) = √40 = 6.32455532,
AC = √((Хc-Хa)²+(Ус-Уa)²) = √16 = 4.
Из этого расчёта видно, что треугольник равнобедренный.
Периметр равен 16,64911064.
2) МЕДИАНЫ ТРЕУГОЛЬНИКА Медиана АM1 из вершины A: Координаты M1(3; -1) Длина AM1 = 4.24264068711928 Медиана BM2 из вершины B: Координаты M2(2; 2) Длина BM2 = 6 Медиана CM3 из вершины C: Координаты M3(1; -1) Длина CM3 = 4.24264068711928
Длины средних линий:
А₁В₁ = АВ/2 = 3.16227766,
В₁С₁ = ВС/2 = 3.16227766,
А₁С₁ = АС/2 = 2.