Докажи, что четырёхугольник ABCD является прямоугольником, найди его площадь, если A(15;3), B(17;5), C(13;9) и D(11;7). SABCD=?

Показать ответ

Ответ:

dabushov95

19.11.2022 22:05

ответ: 39

Искомые числа 16 и 39.

В графу ответа нужно внести 39

Объяснение:

Обозначим, бОльшее число х, меньшее у.

Отметим отдельно, что х, у - натуральные числа, т.е.

$x \in \N; \: y \in \N$

Тогда фразу "разность чисел равна 23" можно представить в виде:

х - у = 23

А фразу "произведение на 1153 меньше суммы их квадратов". так:

х•у = х² + у² - 1153

Получаем систему уравнений:

$\begin{cases} x - y = 23 \small{ \: < = y= x - 23 } \\ xy = {x}^{2} + {y}^{2} - 1153\end{cases} \\$

Произведем замену у на х - 23 во втором уравнении системы

$\begin{cases} y = x - 23 \\ x(x - 23)= {x}^{2} + {( x - 23)}^{2} - 1153\end{cases}$

Решим второе уравнение из системы:

$x^{2} - 23x= {x}^{2} + x^{2} - 2 \cdot23x + 23^{2} - 1153 \\ x^{2} - 23x= 2 {x}^{2} - 46x + 529 - 1153 \\ x^{2} - 23x - 2 {x}^{2} + 46x + 624 = 0 \\ {x}^{2} - 23x - 624 = 0$

Воспользуемся Т. Виета:

$\begin{cases}x_1+x_2=23 \\ x_1 x_2 = -624 \end{cases}$

Число 624 можно представить как произведение чисел 16 и 39

(И что примечательно, разность 39 и 16 равна 23)

624 = 39 • 16

Тогда, если взять за х1 = 39, х2= -16

-624 = 39 • (-16)

$\begin{cases}x_1+x_2= 39 - 16 \\ x_1 x_2 = 39 \cdot ( - 16) \end{cases} \\ \begin{cases}x_1=39 \\ x_2 = -16 \end{cases}$

Так как по условию х, у - натуральные,

то х2 = -16 не подхожит по условию Остается один корень: х = 39.

Подставляем значение х в начальную систему уравнений:

$\begin{cases} y= x - 23 \\ x=39\end{cases} < = \begin{cases} y= 39 - 23 = 16 \\ x=39\end{cases}$

И получим ответ:

$\begin{cases} x = 39 \\ y = 16\end{cases}$

0,0(0 оценок)

Ответ:

мадина3031

06.02.2023 02:17

$15\sqrt{5}$ (кв. единица)

Объяснение:

По условию задано координаты трёх его вершин параллелограмма АВСD: А(27;18;20) , В(24;18;16) и С(18;21;18). Так как верно свойство (см. рисунок) "Диагональ параллелограмма делит его на два равных треугольника", то площадь параллелограмма S(ABCD) равна удвоенной площади одного из треугольников, то есть

S(ABCD)=2·S(ABC).

В нашем случае диагональ AC делит параллелограмм на два равных треугольника. Поэтому достаточно найти площадь S(ABC) треугольника ABC по формуле Герона:

$\tt \displaystyle S(ABC)=\sqrt{p \cdot (p-a) \cdot (p-b) \cdot(p-c) },$

где p - полупериметр: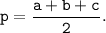 $\tt \displaystyle p=\frac{a+b+c}{2} .$

Стороны треугольника ABC находим по формуле расстояния между двумя точками с координатами M(x₁; y₁; z₁) и N(x₂; y₂; z₂):

$\tt \displaystyle d(MN)=\sqrt{(x_{1} -x_{2} )^{2}+(y_{1} -y_{2} )^{2}+(z_{1} -z_{2} )^{2}} .$

Так как А(27;18;20), В(24;18;16) и С(18;21;18), то

$\tt \displaystyle a=d(AB)=\sqrt{(27-24 )^{2}+(18 -18)^{2}+(20 -16 )^{2}} =\\\\=\sqrt{3^{2}+0^{2}+4^{2}} =\sqrt{9+16} =\sqrt{25} =5;$

$\tt \displaystyle b=d(BC)=\sqrt{(24-18 )^{2}+(18-21)^{2}+(16-18)^{2}} =\\\\=\sqrt{6^{2}+3^{2}+2^{2}} =\sqrt{36+9+4} =\sqrt{49} =7;$

$\tt \displaystyle c=d(AC)=\sqrt{(27-18 )^{2}+(18-21)^{2}+(20-18)^{2}} =\\\\=\sqrt{9^{2}+3^{2}+2^{2}} =\sqrt{81+9+4} =\sqrt{94};$

$\tt \displaystyle p=\frac{5+7+\sqrt{94}}{2}= \frac{12+\sqrt{94}}{2};$

$\tt \displaystyle S(ABC)=\sqrt{\frac{12+\sqrt{94}}{2} \cdot (\frac{12+\sqrt{94}}{2}-5) \cdot (\frac{12+\sqrt{94}}{2}-7) \cdot(\frac{12+\sqrt{94}}{2}-\sqrt{94} ) }=\\\\=\sqrt{\frac{12+\sqrt{94}}{2} \cdot \frac{2+\sqrt{94}}{2} \cdot \frac{-2+\sqrt{94}}{2} \cdot \frac{12-\sqrt{94}}{2}}=\\\\=\sqrt{\frac{144-94}{4} \cdot \frac{-4+94}{4} }=\sqrt{\frac{50}{4} \cdot \frac{90}{4} }=\frac{\sqrt{25\cdot 45}}{\sqrt{2^2} } =\frac{\sqrt{5^2\cdot 3^2\cdot 5}}{2} =\frac{15\cdot\sqrt{5}}{2};$