Докажите,что если в треугольнике две высоты равны,то он является равнобедренным

Показать ответ

Ответ:

Gazizianov2018

17.05.2023 23:45

В прямоугольном треугольнике найти все линейные элементы

Объяснение:

ΔKNT подобен ΔMKT по 2-м углам: ∠МТК=NTK=90, ∠M=∠TKN.

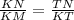Значит сходственные стороны пропорциональны : $\frac{KN}{KM} =\frac{TN}{KT}$ .

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой ⇒ КТ=√( МТ*ТN) .

$\frac{6}{5} =\frac{TN}{\sqrt{MT*TN} }$ , $\frac{6}{5} =\frac{TN}{\sqrt{MT}*\sqrt{TN} }$ , $\frac{6}{5} =\frac{\sqrt{TN} }{\sqrt{MT} }$ , $\frac{36}{25} =\frac{TN}{TM}$ .

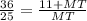Из условия TN=11+MT , поэтому $\frac{36}{25} =\frac{11+MT}{MT}$ , 36MT=25(11+MT) , MT=25. Тогда TN=11+25=36 , гипотенуза MN=25+61=61.

Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и проекций катетов на гипотенузу :

а) катет МК=√(МN*MT) , MK=√(25*61)=5√61;

б) катет КN=√(МN*TN) , KN=√(36*61)=6√61.

в) высота КТ=√( МТ*ТN) , КТ=√( 25*36)=30 .

с задачей. Найдите все линейные элементы , угол К = 90°.

0,0(0 оценок)

Ответ:

198912

16.06.2022 11:28

Третий признак равенства прямоугольных треугольников-если гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого треугольника,то такие треугольники равны между собой

По условию задачи ВЕ=КС,гипотенузы равны

Сумма острых углов в прямоугольных треугольниках составляет 90 градусов

По условию задачи нам дали значение двух разных углов в двух разных треугольниках

В первом треугольнике угол Е равен 75 градусов

Узнаём,чему равен второй острый угол,угол В

<В=90-75=15 градусов

В треугольнике КМС указан острый угол 15 градусов,чему равен второй острый угол?

90-15=75 градусов

В одном треугольнике острые углы равны 15 и 75 градусов,во втором треугольнике острые углы имеют туже градусную меру 15 и 75 градусов

Треугольники ВDE и КМС равны между собой по третьему признаку

Объяснение:

0,0(0 оценок)