Два трикутника симетричні одна одній щодо точки. Два кута
першого трикутника відповідно рівні 30º і 60º. Чи є другий трикутник
прямокутним?Два трикутника симетричні одна одній щодо точки. Два кута
першого трикутника відповідно рівні 30º і 60º. Чи є другий трикутник
прямокутним?
Заметим, что если провести из любой вершины высоту, то она будет и биссектрисой и медианой одновременно. Также точка пересечения медиан будет совпадать с точкой пересечения биссектрис и высот (так как в правильном треугольнике медианы биссектрисы и высоты, проведенные из одной вершины совпадают). А медианы делятся в точке пересечения в соотношении 2 к 1, начиная от вершины. Теперь отрезок медианы от точки пресечения медиан до вершины будет радиусом описанной окружности. А отрезок медианы от точки пересечения медиан до основания (стороны, к которой проведен) будет радиусом вписанной окружности. Значит половина длины радиуса описанной окружности равна длине радиуса вписанной окружности. То есть 8:2=4 см.
ответ: радиус вписанной окружности равен 4 см.
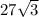 ед².
ед².
Объяснение:Обозначим данную пирамиду буквами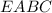 .
.
Проведём высоту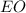 . Точка
. Точка 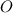 - центр
- центр 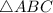 - точка пересечения, медиан, высот и биссектрис треугольника.
- точка пересечения, медиан, высот и биссектрис треугольника.
Проведём апофему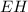 (апофема - это высота боковой грани пирамиды, проведённая из вершины пирамиды) к стороне
(апофема - это высота боковой грани пирамиды, проведённая из вершины пирамиды) к стороне 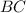 основания пирамиды.
основания пирамиды.
Т.к. данная пирамида - правильная, треугольная ⇒ основание пирамиды - правильный треугольник.
Проведём высоту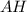 в
в 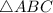 .
.
Т.к.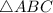 - равносторонний ⇒
- равносторонний ⇒ 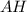 - высота, медиана, биссектриса.
- высота, медиана, биссектриса.
Высота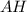 и апофема
и апофема 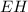 имеют общее основание, а именно точку
имеют общее основание, а именно точку 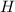 , т.к.
, т.к. 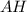 - медиана, а апофема
- медиана, а апофема 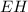 делит
делит 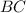 пополам (по свойству).
пополам (по свойству).
Рассмотрим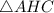 :
:
Найдём высоту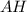 по теореме Пифагора:
по теореме Пифагора: 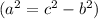
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Точка O - пересечение медиан и делит их в отношении 2 : 1, считая от вершины.
Рассмотрим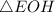 :
:
Если угол прямоугольного треугольника равен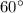 , то напротив лежащий катет равен произведению меньшего катета на
, то напротив лежащий катет равен произведению меньшего катета на 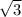 .
.
Найдём апофему по теореме Пифагора: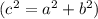
====================================================
⇒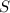 бок. поверх. =
бок. поверх. = 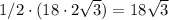 ед².
ед².
⇒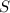 полн. поверх. =
полн. поверх. = 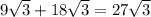 ед².
ед².