Площадь треугольника ABC равна 54 см в квадрате. На стороне AB обозначили точки D и E так, что AD=DE=BE, а на стороне AC - точки M и N так, что AM=MN=NC. Найдите площадь четырехугольника BCNE.
Решение.
Т.к AD=DE=BE и AM=MN=NC , то
ΔAEN~ ΔABC по двум пропорциональным сторонам и равному углу между ними : ∠А-общий, АЕ:АВ=AN:АС=2:3.
Коэффициент подобия к=2/3 .
Отношение площадей подобных треугольников равно к² ⇒
S(AEN):S(ABC)=4:9 или S(AEN):54=4:9 , S(AEN)=24 см²
Площадь треугольника ABC равна 54 см в квадрате. На стороне AB обозначили точки D и E так, что AD=DE=BE, а на стороне AC - точки M и N так, что AM=MN=NC. Найдите площадь четырехугольника BCNE.
Решение.
Т.к AD=DE=BE и AM=MN=NC , то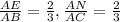
ΔAEN~ ΔABC по двум пропорциональным сторонам и равному углу между ними : ∠А-общий, АЕ:АВ=AN:АС=2:3.
Коэффициент подобия к=2/3 .
Отношение площадей подобных треугольников равно к² ⇒
S(AEN):S(ABC)=4:9 или S(AEN):54=4:9 , S(AEN)=24 см²
S(BCNE)=S(ABC) -S(AEN)=54-24=30 ( см²).
Отрезок AC виден из точки B под данным углом - точка B лежит на некоторой данной дуге.
Задача Архимеда о половине ломаной:
Ломаная A-B-C вписана в дугу ADC, точка D - середина дуги. Докажем, что перпендикуляр DH, опущенный на больший отрезок AB, делит ломаную пополам.
Пусть AE=BC
DA=DC (стягивают равные дуги)
∠DAB=∠DCB (опираются на одну дугу)
△DAE=△DCB => DE=DB
△EDB - р/б, DH - высота и медиана, EH=HB
AE+EH=HB+BC
Теперь видно, что достаточно максимизировать отрезок AH.
В треугольнике ADH катет AH всегда меньше гипотенузы AD. Максимум достигается, когда точки H, D, B совпадают.
То есть, когда B - середина дуги, BA=BC.