Хорда окружности делится пополам её диаметром. докажите, что либо эта хорда перпендикулярна данному диаметру, либо она сама проходит через центр окружности. ​

Дано: А(-3; 9), В(-4; -8), С(6; 0)

Найти:

а)координаты вектора АС;

б)длину вектора ВС;

в)координаты середины отрезка АВ:

г)периметр треугольника АВС;

д)длину медианы СМ.

a) AC = {Cx - Ax ; Cy - Ay}

AC = {6 - (-3) ; 0 - 9}

AC ={9 ; -9}

б) BC = {Cx - Bx ; Cy - By}

BC = {6 - (-4); 0 - (-8)}

BC = {10 ; 8}

|BC| =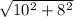 = = 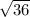6

в) Пусть это будет точка M, тогда её координаты будут равны

M((Ax + Bx)/2 ; (Ay + By)/2)

M((-3 + -4)/2 ; (9 + 8)/2)

M(-3,5 ; 8,5)

г) Посчитаем длину каждой стороны треугольника

AB = = =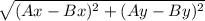

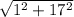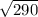
AC = = =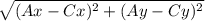

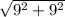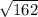
д) СМ = =   =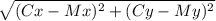

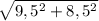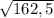
Я отвечу только на второе

Доказательства в объяснении.

Объяснение:

1. Угол КАВ - угол между касательной АК и хордой АВ, проходящей через точку касания А, равен половине градусной меры дуги АВ, заключённой между его сторонами. Вписанный угол АСВ опирается на эту же дугу АВ, а  вписанный угол равен половине градусной меры дуги, на которую он опирается.

Следовательно, ∠АСВ = ∠КАВ, что и требовалось доказать.

2. Т.к. углы АВК И ВАС- это внутренние накрест лежащие при КВ║АС и секущей АВ, то ∠АВК =∠ВАС.   ∠АСВ = ∠КАВ (доказано выше).

По сумме внутренних углов треугольников АВС и КАВ имеем:

∠АВС = 180 - (∠АСВ + ∠ВАС)  

∠АКВ = 180 - (∠КАВ + ∠АВК)   =>

∠АВС = ∠АКВ.  =>  ∠АВК = ∠АКВ  =>

Треугольник КАВ - равнобедренный, так как углы при основании ВК равны. Что и требовалось доказать.  

3. Треугольники АСВ и КАВ подобны по  2 признаку подобия (по двум углам) с коэффициентом подобия k = АС/АВ. (Отношение соответственных сторон треугольников).

Площади подобных треугольников относятся как квадрат коэффициента подобия.

Sabc/Sabk = k² = АС²/АВ².

По теореме косинусов в тр-ке АВС найдем:

АВ²=2АС²-2АС²·Cosα = 2АC²·(1-Cosα).  

Тогда k²=АС²/(2АC²·(1-Cosα)) = 1/(2·(1-Cosα)). =>  

к² зависит только от угла α, то есть  

отношение площадей зависит только от величины угла АСВ.

Что и требовалось доказать.