Пара наклонных имеет один общий перпендикуляр, или один общий катет (CD).
Формула вычисления катета CD (по теореме Пифагора), зная гипотенузу AC, и катет AD:
Формула вычисления катета CD, зная гипотенузу BC, и катет DB:
Объявим катет CD — как переменную "y", составим систему:
Как мы видим — x равен 5-и, тоесть каждая проекция будет больше гипотенузы, так не пойдёт.
Но если в уравнении есть цифры в квадратах (например — x²), то определение переменных имеет 2 вида: цифра или отрицательная, или положительная, чтобы найти правильный вариант — надо решить уравнение ещё раз, но только уже с известными двумя типами.
Как видим, x — не может быть равен 5-и, что и означает, что он равен -5-и.
Убедимся в этом:
Ни в коем случае не считаем 16x & 9x — как абсолютные длины проекций, ведь если AD = 9x, то: AD = -5*9 = -45.
А если с цифрой -45, и перпендикуляром 25 — попробовать найти гипотенузу(), то ничего не получится.
//Это точно правильный ответ — посчитав сама, и даже проверив онлайн калькуляторами.
АВ = Рabcd : 4 = 12 : 4 = 3 см ВВ₁ и DD₁ - медианы, значит AD₁ = D₁B = AB₁ = B₁D = 3/2 см
ΔABD равнобедренный, поэтому ∠ABD = ∠ADB, BD₁ = DB₁, BD - общая сторона для ΔDD₁B и ΔBB₁D, значит эти треугольники равны по двум сторонам и углу между ними, ⇒ BB₁ = DD₁.
Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины. Обозначим OD₁ = OB₁ = x, тогда OD = OB = 2x. ΔOBD равнобедренный, значит ∠OBD = ∠ODB = 40°. ∠D₁OB = ∠OBD + ∠ODB = 80° как внешний угол ΔDOB.
Если необходимо числовое значение, а не выражение, можно взять значение cos 80° по таблице, тогда получится: cos 80° ≈ 0,1736 BB₁ = 9 / (2√(5 - 4cos80°)) ≈ 2,2
25.
Отношения проекций такова: 9:16.
Тоесть их переменные таковы: AD = 9x; DB = 16x.
Пара наклонных имеет один общий перпендикуляр, или один общий катет (CD).
Формула вычисления катета CD (по теореме Пифагора), зная гипотенузу AC, и катет AD: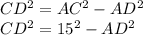
Формула вычисления катета CD, зная гипотенузу BC, и катет DB: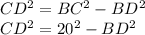
Объявим катет CD — как переменную "y", составим систему:
Как мы видим — x равен 5-и, тоесть каждая проекция будет больше гипотенузы, так не пойдёт.
Но если в уравнении есть цифры в квадратах (например — x²), то определение переменных имеет 2 вида: цифра или отрицательная, или положительная, чтобы найти правильный вариант — надо решить уравнение ещё раз, но только уже с известными двумя типами.
Как видим, x — не может быть равен 5-и, что и означает, что он равен -5-и.
Убедимся в этом:
Ни в коем случае не считаем 16x & 9x — как абсолютные длины проекций, ведь если AD = 9x, то: AD = -5*9 = -45.
А если с цифрой -45, и перпендикуляром 25 — попробовать найти гипотенузу(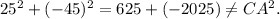
), то ничего не получится.
//Это точно правильный ответ — посчитав сама, и даже проверив онлайн калькуляторами.
Вывод: x = -5; CD = 25.
29.
Углы, образующийся наклонными, и прямой: <ADB = 30°; <ACB = 60°.
Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Против угла ADB — лежит расстояние между точкой A — до прямой, тоесть перпендикуляр, та же высота, тот же катет AB.
Тоесть: AB = AD/2 ⇒ AD = AB*2 = 32.
<ACB = 60° => <CAB = 90-60 = 30°.
Та жа теорема: <CAB = 30° => CB = CA/2.
По теореме Пифагора: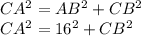
Так как катет AB — равен половине гипотенузы, то объявим обе неизвесные числа, как переменная "x":
Вывод: AD = 32; AC = 18.5.
ВВ₁ и DD₁ - медианы, значит
AD₁ = D₁B = AB₁ = B₁D = 3/2 см
ΔABD равнобедренный, поэтому
∠ABD = ∠ADB,
BD₁ = DB₁, BD - общая сторона для ΔDD₁B и ΔBB₁D, значит эти треугольники равны по двум сторонам и углу между ними, ⇒
BB₁ = DD₁.
Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины.
Обозначим OD₁ = OB₁ = x, тогда OD = OB = 2x.
ΔOBD равнобедренный, значит ∠OBD = ∠ODB = 40°.
∠D₁OB = ∠OBD + ∠ODB = 80° как внешний угол ΔDOB.
Рассмотрим ΔD₁OB. По теореме косинусов
D₁B² = OD₁² + OB² - 2·OD₁·OB·cos 80°
9/4 = x² + 4x² - 2 · x · 2x · cos80°
9/4 = 5x² - 4x² · cos80°
9/4 = x² (5 - 4cos80°)
x² = 9 / (4(5 - 4cos80°))
x = 3 / (2√(5 - 4cos80°))
BB₁ = 3x = 9 / (2√(5 - 4cos80°)) или
Если необходимо числовое значение, а не выражение, можно взять значение cos 80° по таблице, тогда получится:
cos 80° ≈ 0,1736
BB₁ = 9 / (2√(5 - 4cos80°)) ≈ 2,2