Дан куб A…D1 с ребром a. Найдите угол между плоскостью AB1 D1 и плоскостью диагонального сечения грани BDD1 B1 . Тема: двугранный угол.
Объяснение:
Определим двугранный угол между плоскостями AB₁D₁и BDD₁B₁. Эти плоскости пересекаются по прямой D₁B₁. Найдем два перпендикуляра к этой прямой , выходящие из одной точки.
Пусть О₁и О- точки пересечения диагоналей верхней и нижней граней соответственно . Тогда D₁О=ОB₁. Значит медиана АО ,в равнобедренном ΔAB₁D₁, является высотой ⇒АО₁⊥B₁D₁,
О₁О║В₁В ⇒О₁О⊥B₁D₁. Поэтому ∠АО₁О-линейный угол данного двугранного.
если <ВАС=120°, то ВС является основанием треугольника АВС, а АС и АВ - боковыми сторонами. Медиана АН, проведённая из вершины угла А к основанию ВС является ещё высотой и биссектрисой, которая образует два равных прямоугольных треугольника ВАН и САН, в которых АВ и АС - гипотенузы, а ВН, СН и медиана АН - катеты, поэтому <САН=<ВАН=120÷2=60° и <АНВ=<АНС=90°. Сумма острых углов прямоугольного треугольника составляет 90°, поэтому <АВН=<АСН=90–60=30°. Медиана-катет, лежащая напротив угла 30° равна половине гипотенузы поэтому АН=20÷2=10см
ОТВЕТ: АН=10см
ЗАДАНИЕ 11
а) Если АВ и СД параллельны, то <АСД=<KCN=110° и внутренний угол АВД= внешнему углу В
ABСД- четырёхугольник, при котором две противоположные стороны параллельны и 2 противоположных угла равны (по условиям), следовательно этот четырёхугольник - параллелограмм, поэтому АС || ВД
б) если провести отрезок АД, то получится равнобедренный треугольник АСД, в котором АД - основание, а АС = ВД. и являются боковыми сторонами, поэтому углы при основании САД и СДА равны. Сумма углов треугольника составляет 180°, поэтому <САД=<СДА=(180–110)÷2=70÷2=35°.
ОТВЕТ: углы ∆ДАС (САД=СДА)=35°
в) если можно использовать предыдущие данные, что АС=АД, то четырёхугольник АВСД- ромб, у которого все стороны равны, поскольку в задании а) мы выяснили, что АВСД- параллелограмм и если АС=АД,=АВ=ВД=18см, тогда периметр ромба=18×4=72см
Дан куб A…D1 с ребром a. Найдите угол между плоскостью AB1 D1 и плоскостью диагонального сечения грани BDD1 B1 . Тема: двугранный угол.
Объяснение:
Определим двугранный угол между плоскостями AB₁D₁и BDD₁B₁. Эти плоскости пересекаются по прямой D₁B₁. Найдем два перпендикуляра к этой прямой , выходящие из одной точки.
Пусть О₁и О- точки пересечения диагоналей верхней и нижней граней соответственно . Тогда D₁О=ОB₁. Значит медиана АО ,в равнобедренном ΔAB₁D₁, является высотой ⇒АО₁⊥B₁D₁,
О₁О║В₁В ⇒О₁О⊥B₁D₁. Поэтому ∠АО₁О-линейный угол данного двугранного.
ΔАО₁О-прямоугольный , tg (∠АО₁О)=АО/О₁О , tg (∠АО₁О)=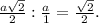 /
/
∠АО₁О=arctg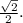
====================================================
1)Диагонали любой грани куба равны и находятся по т. Пифагора √(а²+а²)=√2а²=а√2 . Половина диагонали равна(а√2) /2
2)ΔAB₁D₁, -равнобедренном, т.к. В₁А=АD.
Объяснение:
ЗАДАНИЕ 10
если <ВАС=120°, то ВС является основанием треугольника АВС, а АС и АВ - боковыми сторонами. Медиана АН, проведённая из вершины угла А к основанию ВС является ещё высотой и биссектрисой, которая образует два равных прямоугольных треугольника ВАН и САН, в которых АВ и АС - гипотенузы, а ВН, СН и медиана АН - катеты, поэтому <САН=<ВАН=120÷2=60° и <АНВ=<АНС=90°. Сумма острых углов прямоугольного треугольника составляет 90°, поэтому <АВН=<АСН=90–60=30°. Медиана-катет, лежащая напротив угла 30° равна половине гипотенузы поэтому АН=20÷2=10см
ОТВЕТ: АН=10см
ЗАДАНИЕ 11
а) Если АВ и СД параллельны, то <АСД=<KCN=110° и внутренний угол АВД= внешнему углу В
ABСД- четырёхугольник, при котором две противоположные стороны параллельны и 2 противоположных угла равны (по условиям), следовательно этот четырёхугольник - параллелограмм, поэтому АС || ВД
б) если провести отрезок АД, то получится равнобедренный треугольник АСД, в котором АД - основание, а АС = ВД. и являются боковыми сторонами, поэтому углы при основании САД и СДА равны. Сумма углов треугольника составляет 180°, поэтому <САД=<СДА=(180–110)÷2=70÷2=35°.
ОТВЕТ: углы ∆ДАС (САД=СДА)=35°
в) если можно использовать предыдущие данные, что АС=АД, то четырёхугольник АВСД- ромб, у которого все стороны равны, поскольку в задании а) мы выяснили, что АВСД- параллелограмм и если АС=АД,=АВ=ВД=18см, тогда периметр ромба=18×4=72см
ОТВЕТ: Р=72см