По определению, две прямые параллельны, если существует плоскость в которой лежат две эти прямые, и они там параллельны. Отметим на данной прямой точки A и B. А точку обозначим как O. Пусть через точку О проходят две прямые параллельные AB. Пусть -- плоскость, содержащая одновременно и AB (эта плоскость существует из определения). Аналогично определяем плоскость . Заметим, что и проходят через точки O, A, B. Но по аксиоме через три точки, не лежащие на одной прямой проходит только одна плоскость. Значит плоскости = S совпадают. (назовём их общим именем S). Рассмотрим плоскость S: в ней лежат точки O, A, B и две прямые . Причем, проходят через точку O и параллельны AB. Но по аксиоме планиметрии (напомню, мы сейчас живем в плоскости S для которой выполнены все аксиомы планиметрии) через точку O может проходить лишь одна прямая, параллельная AB. Значит , ч.т.д.
Через две точки можно провести прямую линию и притом только одну.
Аксиома 2
Если две точки прямой принадлежат плоскости, то и каждая точка этой прямой принадлежит плоскости.
Аксиома 3
Отрезок прямой короче всякой другой линии (ломаной или кривой), соединяющей его концы.
Расстояние между двумя точками измеряется по прямой линии. В геометрии используются еще и такие аксиомы, которые уже применялись в арифметике и алгебре (сформулируем их для произвольных величин A, B и C):
Объяснение:
По определению, две прямые параллельны, если существует плоскость в которой лежат две эти прямые, и они там параллельны. Отметим на данной прямой точки A и B. А точку обозначим как O. Пусть через точку О проходят две прямые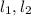
параллельные AB. Пусть 
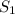-- плоскость, содержащая одновременно 
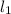и AB (эта плоскость существует из определения). Аналогично определяем плоскость 
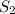. Заметим, что 
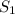и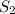 
проходят через точки O, A, B. Но по аксиоме через три точки, не лежащие на одной прямой проходит только одна плоскость. Значит плоскости 
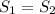= S совпадают. (назовём их общим именем S). Рассмотрим плоскость S: в ней лежат точки O, A, B и две прямые 
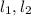. Причем, 
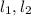проходят через точку O и параллельны AB. Но по аксиоме планиметрии (напомню, мы сейчас живем в плоскости S для которой выполнены все аксиомы планиметрии) через точку O может проходить лишь одна прямая, параллельная AB. Значит 
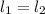, ч.т.д.
Аксиома 1
Через две точки можно провести прямую линию и притом только одну.
Аксиома 2
Если две точки прямой принадлежат плоскости, то и каждая точка этой прямой принадлежит плоскости.
Аксиома 3
Отрезок прямой короче всякой другой линии (ломаной или кривой), соединяющей его концы.
Расстояние между двумя точками измеряется по прямой линии. В геометрии используются еще и такие аксиомы, которые уже применялись в арифметике и алгебре (сформулируем их для произвольных величин A, B и C):
Аксиома 4
Если A=B и B=C, то A=C.
Аксиома 5
Если A=B, то A+C=B+C и A-C=B-C.
Объяснение:
здесь ответы