к сторонам AC и ВС треугольника ABC восстановлены серединные перпендикуляры , пересекающиеся в точке О ; АВ 20 см , угол АОВ 120 градусов . Найдите длину отрезка ОС
Отрежем от ромба его диагональю треугольник. Если ромб был АВСД, то берём треугольник АВС. Он равнобедренный, т.к. АВ=ВС. Значит отрезок, соединяющий середины сторон АВ и ВС является средней линией равнобедренного треугольника, а значит этот отрезок параллелен основанию АС. Аналогично повторяем рассуждения для треугольника AДС, и понимаем, что отрезок, соединяющий середины сторон АД и ДС есть средняя линия, значит он параллелен АС. Итак, имеем, что обе средние линии - треугольников АВС и АДС параллельны диагонали ромба АС, следовательно они параллельны друг другу.
Повторяем те же рассуждения для второй диагонали ромба - ВД, и так же получаем параллельность второй пары отрезков.
Следовательно, четырёхугольник, вершинами которого являются середины сторон ромба, является параллелограммом.
Далее, из симметрии ромба, замечаем, что обе диагонали этого получившегося четырёхугольника проходят через центр ромба, и равны между собой.
Параллелограмм, у которого диагонали равны - это и есть прямоугольник - что и требовалось доказать.
Ну, я бы так доказывал. Может кто-нибудь предложит более простой
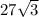 ед².
ед².
Объяснение:Обозначим данную пирамиду буквами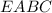 .
.
Проведём высоту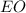 . Точка
. Точка 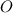 - центр
- центр 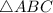 - точка пересечения, медиан, высот и биссектрис треугольника.
- точка пересечения, медиан, высот и биссектрис треугольника.
Проведём апофему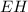 (апофема - это высота боковой грани пирамиды, проведённая из вершины пирамиды) к стороне
(апофема - это высота боковой грани пирамиды, проведённая из вершины пирамиды) к стороне 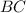 основания пирамиды.
основания пирамиды.
Т.к. данная пирамида - правильная, треугольная ⇒ основание пирамиды - правильный треугольник.
Проведём высоту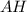 в
в 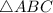 .
.
Т.к.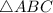 - равносторонний ⇒
- равносторонний ⇒ 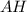 - высота, медиана, биссектриса.
- высота, медиана, биссектриса.
Высота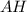 и апофема
и апофема 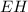 имеют общее основание, а именно точку
имеют общее основание, а именно точку 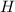 , т.к.
, т.к. 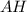 - медиана, а апофема
- медиана, а апофема 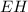 делит
делит 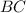 пополам (по свойству).
пополам (по свойству).
Рассмотрим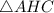 :
:
Найдём высоту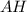 по теореме Пифагора:
по теореме Пифагора: 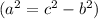
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Точка O - пересечение медиан и делит их в отношении 2 : 1, считая от вершины.
Рассмотрим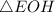 :
:
Если угол прямоугольного треугольника равен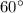 , то напротив лежащий катет равен произведению меньшего катета на
, то напротив лежащий катет равен произведению меньшего катета на 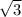 .
.
Найдём апофему по теореме Пифагора: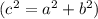
====================================================
⇒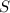 бок. поверх. =
бок. поверх. = 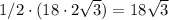 ед².
ед².
⇒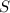 полн. поверх. =
полн. поверх. = 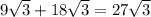 ед².
ед².
Аналогично повторяем рассуждения для треугольника AДС, и понимаем, что отрезок, соединяющий середины сторон АД и ДС есть средняя линия, значит он параллелен АС.
Итак, имеем, что обе средние линии - треугольников АВС и АДС параллельны диагонали ромба АС, следовательно они параллельны друг другу.
Повторяем те же рассуждения для второй диагонали ромба - ВД, и так же получаем параллельность второй пары отрезков.
Следовательно, четырёхугольник, вершинами которого являются середины сторон ромба, является параллелограммом.
Далее, из симметрии ромба, замечаем, что обе диагонали этого получившегося четырёхугольника проходят через центр ромба, и равны между собой.
Параллелограмм, у которого диагонали равны - это и есть прямоугольник - что и требовалось доказать.
Ну, я бы так доказывал. Может кто-нибудь предложит более простой