1) Проведём две высоты к плоскости ABCD из вершин и И отметим их как и соответственно.
2)Рассмотрим полученный треугольник ; По чертежу видно, что этот треугольник прямоугольный и один из его острых углов равен 60 градусов, что означает что второй его угол равен 30 градусам, следовательно если нам известна , то можно и найти
(Против угла в 30 градусов лежит катет равный половине гипотенузы).
3)Поскольку пирамида правильная, то высоты, которые были проведены в 1 пункте делят диагональ квадрата ABCD на 3 отрезка, причем
4) Используя правило прямоугольного треугольника, при двух его известных сторонах и углу, можно найти другую сторону этого треугольника:
5)Следует детально рассмотреть треугольник В нем известны две стороны, и он прямоугольный, а значит можно найти по теореме Пифагора. .
6)Отсюда можно найти .
. Знаю эту величину можем найти искомую АB.
Поскольку в основании правильной усеченной четырёхугольной пирамиды лежит квадрат. ; Но также стоит заметить, что , но второй намного легче, чем мучиться с преобразованием корневых выражений.
Задача: Треугольник ABC и DEF — равнобедренные. AB || DE, ∠ABC = 80°. Определить величину угла PHF.
Т.к. ΔABC равнобедренный (AB = BC), имея угол ABC, равный 80°, определим углы при основе AC:
∠BAC = ∠BCA = (180−80)/2 = 100/2 = 50°
∠BAC = ∠EDF = 50° — как соответственные при параллельных прямых AB и DE и секущей AF.
Т.к. ΔDEF равнобедренный (DE = EF), ∠EDF = ∠EFD = 50°.
Р-м ΔHFP:
∠FPH = 90°, PFH = 50° ⇒
⇒ ∠PHF = 180−∠FPH−∠PFH = 180−90−50 = 40°
ответ: Величина угла PHF равна 40°.
Задача: Треугольник ABC и BDC — равнобедренные. ∠BAC = 86°. Определить величину угла ACD.
Т.к. ΔABC равнобедренный (AB = AC), имея угол BAC, равный 86°, определим углы при основе BC:
∠ABC = ∠ACB = (180−86)/2 = 94/2 = 47°
Р-м ΔBDC:
Обозначим отрезок, соединяющий вершину D и сторону BC через DH.
BC = 1/2DH ⇒ DH — медиана
Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным, а медина проведена из прямого угла к гипотенузе ⇒
⇒ ΔBDC — прямоугольный, ∠BDC = 90°.
Т.к. ΔBDC равнобедренный (BD = CD), имея угол BDC, равный 90°, определим углы при основе BC:
Дано:
Найти: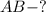
1) Проведём две высоты к плоскости ABCD из вершин
и 
И 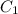отметим их как 
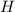и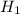 
соответственно.
2)Рассмотрим полученный треугольник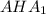
; По чертежу видно, что этот треугольник прямоугольный и один из его острых углов равен 60 градусов, что означает что второй его угол равен 30 градусам, следовательно если нам известна 
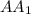, то можно и найти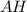 
3)Поскольку пирамида правильная, то высоты, которые были проведены в 1 пункте делят диагональ квадрата ABCD на 3 отрезка, причем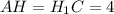
4) Используя правило прямоугольного треугольника, при двух его известных сторонах и углу, можно найти другую сторону этого треугольника: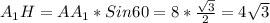
5)Следует детально рассмотреть треугольник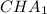
В нем известны две стороны, и он прямоугольный, а значит можно найти 
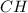по теореме Пифагора. 
.
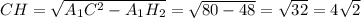6)Отсюда можно найти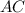
.
Поскольку в основании правильной усеченной четырёхугольной пирамиды лежит квадрат.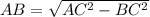
; Но также стоит заметить, что 
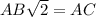, но второй намного легче, чем мучиться с преобразованием корневых выражений.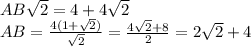 
ответ: AB= двум корней из двух плюс 4
Задача: Треугольник ABC и DEF — равнобедренные. AB || DE, ∠ABC = 80°. Определить величину угла PHF.
Т.к. ΔABC равнобедренный (AB = BC), имея угол ABC, равный 80°, определим углы при основе AC:
∠BAC = ∠BCA = (180−80)/2 = 100/2 = 50°
∠BAC = ∠EDF = 50° — как соответственные при параллельных прямых AB и DE и секущей AF.
Т.к. ΔDEF равнобедренный (DE = EF), ∠EDF = ∠EFD = 50°.
Р-м ΔHFP:
∠FPH = 90°, PFH = 50° ⇒
⇒ ∠PHF = 180−∠FPH−∠PFH = 180−90−50 = 40°
ответ: Величина угла PHF равна 40°.
Задача: Треугольник ABC и BDC — равнобедренные. ∠BAC = 86°. Определить величину угла ACD.
Т.к. ΔABC равнобедренный (AB = AC), имея угол BAC, равный 86°, определим углы при основе BC:
∠ABC = ∠ACB = (180−86)/2 = 94/2 = 47°
Р-м ΔBDC:
Обозначим отрезок, соединяющий вершину D и сторону BC через DH.
BC = 1/2DH ⇒ DH — медиана
Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным, а медина проведена из прямого угла к гипотенузе ⇒
⇒ ΔBDC — прямоугольный, ∠BDC = 90°.
Т.к. ΔBDC равнобедренный (BD = CD), имея угол BDC, равный 90°, определим углы при основе BC:
∠DBC = ∠DCB = (180−90)/2 = 90/2 = 45°
Итого, ∠ACD будет равен:
∠ACD = ∠ACB+∠BCD = 47+45 = 92°
ответ: Величина угла ACD равна 92°.