1) Основание прямой призмы – прямоугольный треугольник с гипотенузой 15см и катетом 12см. Найдите площадь боковой поверхности, если грань содержащая больший катет – квадрат. Решение. По Пифагору найдем второй катет основания призмы: √(15²-12²)=√(27*3)=9см. Следовательно, больший катет равен 12см и высота призмы равна 12см (так как боковая грань - квадрат 12х12 - дано). Площадь боковой поверхности призмы равна Sб=P*h, где Р - периметр, а h - высота призмы. Sб=36*12=432см².
2) Ребро правильного тетраэдра равно а. Постройте сечение плоскостью, проходящей через ребро АС и делящее его в отношении 1:2, и проходящей параллельно ребру АВ. Решение. Условие для однозначного решения не полное. Во-первых, не понятно условие "Постройте сечение плоскостью, проходящей через ребро АС и делящее его в отношении 1:2". Проходящее - содержащее это ребро или пересекающее его? Раз сечение делит ребро в отношении 1:2, значит плоскость пересекает это ребро и делит его в отношении 1:2, но считая от какой вершины? Во вторых, таких сечений может быть бесконечное множество, так как плоскость, параллельная прямой АВ, может пересекать тетраэдр в любом направлении. Например, параллельно грани АВS (сечение MNP) или проходящее через точку Q на ребре AS (сечение MQDN). Причем линия пересечения грани АSB и плоскости сечения будет параллельна ребру АВ. Вывод: однозначного решения по задаче с таким условием нет.
Найдем, как связаны радиусы вписанных окружностей.
Пусть сторона правильного треугольника равна a.
Сначала нужно найти длину отрезка AD. Проще всего это сделать по теореме косинусов.
Посмотрим на треугольник ABD. В нем BD = 7/15 a, AB = a, угол B = 60 градусов.
Тогда ,
AD = 13/15 a
Периметр треугольника ACD = a + 8/15 a + 13/15 a = 36/15 a, треугольника ABD = a + 7/15 a + 13/15 a = 35/15 a.
С одной стороны, площадь треугольника - половина прооизведения высоты на сторону, с другой - половина произведения периметра на радиус списанной окружности. Если считать по первой формуле, получим, что S1/S2 = CD/DB = 8/7 (здесь индекс 1 соответствует треугольнику ACD). По второй: S1/S2 = (36*r1)/(35*r2).
Итак,
Площади кругов пропорциональны квадратам радиусов, поэтому площади относятся как 100 к 81.
Есдиственный вопрос, площадь какого из кругов дана. Отсюда и 2 ответа: 81*100/81=100 или 81*81/100=65.61
Решение.
По Пифагору найдем второй катет основания призмы:
√(15²-12²)=√(27*3)=9см.
Следовательно, больший катет равен 12см и высота призмы равна 12см (так как боковая грань - квадрат 12х12 - дано).
Площадь боковой поверхности призмы равна Sб=P*h, где Р - периметр, а h - высота призмы.
Sб=36*12=432см².
2) Ребро правильного тетраэдра равно а. Постройте сечение плоскостью, проходящей через ребро АС и делящее его в отношении 1:2, и проходящей параллельно ребру АВ.
Решение.
Условие для однозначного решения не полное.
Во-первых, не понятно условие "Постройте сечение плоскостью, проходящей через ребро АС и делящее его в отношении 1:2".
Проходящее - содержащее это ребро или пересекающее его?
Раз сечение делит ребро в отношении 1:2, значит плоскость пересекает это ребро и делит его в отношении 1:2, но считая от какой вершины?
Во вторых, таких сечений может быть бесконечное множество, так как плоскость, параллельная прямой АВ, может пересекать тетраэдр в любом направлении. Например, параллельно грани АВS (сечение MNP) или проходящее через точку Q на ребре AS (сечение MQDN).
Причем линия пересечения грани АSB и плоскости сечения будет параллельна ребру АВ.
Вывод: однозначного решения по задаче с таким условием нет.
Найдем, как связаны радиусы вписанных окружностей.
Пусть сторона правильного треугольника равна a.
Сначала нужно найти длину отрезка AD. Проще всего это сделать по теореме косинусов.
Посмотрим на треугольник ABD. В нем BD = 7/15 a, AB = a, угол B = 60 градусов.
Тогда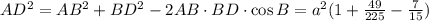 ,
,
AD = 13/15 a
Периметр треугольника ACD = a + 8/15 a + 13/15 a = 36/15 a, треугольника ABD = a + 7/15 a + 13/15 a = 35/15 a.
С одной стороны, площадь треугольника - половина прооизведения высоты на сторону, с другой - половина произведения периметра на радиус списанной окружности. Если считать по первой формуле, получим, что S1/S2 = CD/DB = 8/7 (здесь индекс 1 соответствует треугольнику ACD). По второй: S1/S2 = (36*r1)/(35*r2).
Итак,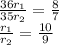
Площади кругов пропорциональны квадратам радиусов, поэтому площади относятся как 100 к 81.
Есдиственный вопрос, площадь какого из кругов дана. Отсюда и 2 ответа: 81*100/81=100 или 81*81/100=65.61
ответ: 100 или 65,61.