Решение очень простое - вся "хитрость" в том, что угол О1АО2 (между пунктирными прямыми) равен 90 градусам. Дело в том, что О1А и О2А - биссеткриссы смежных углов (почему биссектрисы, - это понятно? обоснуйте), а сумма смежных углов 180 градусов. Ну, сумма половин смежных углов (то есть сумма угла О1АВ и угла О2АВ) дает 90.
Таким образом, трегольник О1АО2 - прямоугольный, и АВ - высота к гипотенузе.
Дальше - очень полезное "заклинание" - хотя и очень простое.
Высота к гипотенузе делит прямоугольный треугольник на два, подобные ему - и между собой тоже, конечно.
Пусть точка P(x₀, y₀) удовлетворяет системе уравнений. Возьмём квадратный корень из левой и правой части каждого уравнения:
Первое уравнение задаёт расстояние от точки P(x₀, y₀) до точки A(-4, -3), равное трём. Второе уравнение задаёт расстояние от точки P(x₀, y₀) до точки B(-1, 1), равное двум.
Заметим, что расстояние между точками A(-4, -3) и B(-1, 1) равно . Расстояние между данными точками равно сумме расстояний между точками P(x₀, y₀) и A(-4, -3) и между точками P(x₀, y₀) и B(-1, 1) (AB (5) = AP (3) + PB (2)). Значит, точка P(x₀, y₀) находится на отрезке между точками A(-4, -3) и B(-1, 1) и делит его в отношении 3 : 2, считая от точки A(-4, -3). Тогда справедливо
Поскольку точка A находится не в начале координат, выполнив параллельный перенос на вектор , мы получим координаты точки P(x₀, y₀): .
вот вам рисунок
Решение очень простое - вся "хитрость" в том, что угол О1АО2 (между пунктирными прямыми) равен 90 градусам. Дело в том, что О1А и О2А - биссеткриссы смежных углов (почему биссектрисы, - это понятно? обоснуйте), а сумма смежных углов 180 градусов. Ну, сумма половин смежных углов (то есть сумма угла О1АВ и угла О2АВ) дает 90.
Таким образом, трегольник О1АО2 - прямоугольный, и АВ - высота к гипотенузе.
Дальше - очень полезное "заклинание" - хотя и очень простое.
Высота к гипотенузе делит прямоугольный треугольник на два, подобные ему - и между собой тоже, конечно.
Поэтому
О1B/АВ = АВ/О2В;
О1B = АВ^2/O2B = 6^2/4 = 9;
(-2,2; -0,6)
Объяснение:
Пусть точка P(x₀, y₀) удовлетворяет системе уравнений. Возьмём квадратный корень из левой и правой части каждого уравнения:
Первое уравнение задаёт расстояние от точки P(x₀, y₀) до точки A(-4, -3), равное трём. Второе уравнение задаёт расстояние от точки P(x₀, y₀) до точки B(-1, 1), равное двум.
Заметим, что расстояние между точками A(-4, -3) и B(-1, 1) равно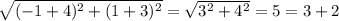
. Расстояние между данными точками равно сумме расстояний между точками P(x₀, y₀) и A(-4, -3) и между точками P(x₀, y₀) и B(-1, 1) (AB (5) = AP (3) + PB (2)). Значит, точка P(x₀, y₀) находится на отрезке между точками A(-4, -3) и B(-1, 1) и делит его в отношении 3 : 2, считая от точки A(-4, -3). Тогда справедливо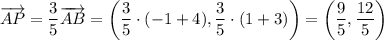 
Поскольку точка A находится не в начале координат, выполнив параллельный перенос на вектор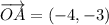
, мы получим координаты точки P(x₀, y₀): 
.
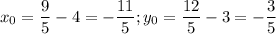Решением системы является точка (-2,2; -0,6).