Медиана, проведенная к боковой стороне равнобедренного RQS, разбивает его на два треугольника так, что периметр одного треугольника на 2см меньше периметра другого. Основание треугольника равно 16см. Найти боковую сторону данного треугольника.
Достаточно убедиться, что сумма квадратов катетов равна квадрату гипотенузы. Для этого считаем квадраты всех отрезков. АВ^2 = 0^2 + 2^2 + 6^2 = 40 BC^2 = 4^2 + 5^2 + 3 ^2 = 50 AC^2 = 4^2 + 7^2 + 3^2 = 74 Видно, что квадрат АС меньше суммы двух других квадратов. Треугольник остроугольный Если ты ошибся в условии и точка B имеет по z координату не 9, а 8, тогда треугольник будет прямоугольным АВ^2 = 29 BC^2 = 45 AC^2 = 74 Если нужно будет,то могу потом скинуть подробное решение,но треугольник по твоим координатам всё равно выходит-остроугольным
В равнобедренной трапеции боковые стороны равны,поэтому равны и углы при основаниях.Сумма боковых углов,односторонних равна 180 °,поэтому 268 °-это сумма тупых углов при основании.Сумма всех углов трапеции равна 360°.
Найти меньший угол трапеции можно двумя
1)Из суммы всех углов 360° вычесть суммы тупых углов 268° и разницу разделить на 2 (угла):
°
2)Сумма боковых углов,односторонних равна 180 °,в условии-тупые углы при основаниях и их сумма равна 268°.
АВ^2 = 0^2 + 2^2 + 6^2 = 40
BC^2 = 4^2 + 5^2 + 3 ^2 = 50
AC^2 = 4^2 + 7^2 + 3^2 = 74
Видно, что квадрат АС меньше суммы двух других квадратов.
Треугольник остроугольный
Если ты ошибся в условии и точка B имеет по z координату не 9, а 8, тогда треугольник будет прямоугольным
АВ^2 = 29
BC^2 = 45
AC^2 = 74
Если нужно будет,то могу потом скинуть подробное решение,но треугольник по твоим координатам всё равно выходит-остроугольным
В равнобедренной трапеции боковые стороны равны,поэтому равны и углы при основаниях.Сумма боковых углов,односторонних равна 180 °,поэтому 268 °-это сумма тупых углов при основании.Сумма всех углов трапеции равна 360°.
Найти меньший угол трапеции можно двумя
1)Из суммы всех углов 360° вычесть суммы тупых углов 268° и разницу разделить на 2 (угла):
2)Сумма боковых углов,односторонних равна 180 °,в условии-тупые углы при основаниях и их сумма равна 268°.
Один угол равен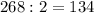 °.
°.
ответ:меньший угол трапеции равен 46 °.