Маленькое замечание. Понятно, что диагональ, на которую опущен перпендикуляр, равна . Но число, фигурирующее в ответе и получающееся при решении задачи, — бОльшая диагональ, значит именно она лежит против тупого угла параллелограмма. Получается, что в условии фраза «перпендикуляр, проведенный из вершины тупого угла» ложна.
Пусть высота , проведенная к диагонали , делит ее на отрезки и .
Так как периметр параллелограмма состоит из двух пар равных сторон, то сумма двух смежных сторон параллелограмма равна . Пусть , тогда .
По теореме Пифагора из треугольника
а из треугольника
Приравнивая полученные выражения, получаем
Тогда
Если из вершины опустить перпендикуляр на диагональ , то треугольники и будут равны, , значит , а
Диагонали параллелограмма равны 14 и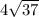
Объяснение:
Маленькое замечание. Понятно, что диагональ, на которую опущен перпендикуляр, равна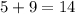 . Но число, фигурирующее в ответе и получающееся при решении задачи,
. Но число, фигурирующее в ответе и получающееся при решении задачи, 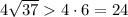 — бОльшая диагональ, значит именно она лежит против тупого угла параллелограмма. Получается, что в условии фраза «перпендикуляр, проведенный из вершины тупого угла» ложна.
— бОльшая диагональ, значит именно она лежит против тупого угла параллелограмма. Получается, что в условии фраза «перпендикуляр, проведенный из вершины тупого угла» ложна.
Пусть высота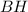 , проведенная к диагонали
, проведенная к диагонали 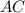 , делит ее на отрезки
, делит ее на отрезки 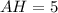 и
и 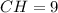 .
.
Так как периметр параллелограмма состоит из двух пар равных сторон, то сумма двух смежных сторон параллелограмма равна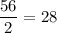 . Пусть
. Пусть 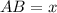 , тогда
, тогда 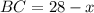 .
.
По теореме Пифагора из треугольника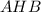
а из треугольника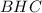
Приравнивая полученные выражения, получаем
Тогда
Если из вершины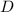 опустить перпендикуляр на диагональ
опустить перпендикуляр на диагональ 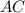 , то треугольники
, то треугольники 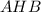 и
и 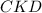 будут равны,
будут равны, 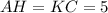 , значит
, значит 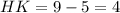 , а
, а
Из треугольника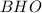 по теореме Пифагора
по теореме Пифагора
Тогда вторая диагональ параллелограмма
30.51
1. Г
2. Д
3, В
30.52
1. Б
2. В
3, Д
Объяснение:
30.51
Зная три стороны треугольника можно найти его площадь по формуле Герона:
где р - полупериметр треугольника,
Затем можно найти радиус вписанной окружности по формуле:
1. а = 5 см, b = 6 см, с = 7 см.
ответ: Г.
2. а = 4 см, b = 6 см, с = 8 см.
ответ: Д.
3. а = 12 см, b = 16 см, с = 20 см.
ответ: В.
30.52
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.1. S₁ : S₂ = 100, ⇒ k² = 100
k = 10
ответ: Б.
2. S₁ : S₂ = 64, ⇒ k² = 64
k = 8
ответ: В.
3. S₁ : S₂ = 25, ⇒ k² = 25
k = 5
ответ: Д.