Может ли луч Om проходить между сторонами угла aob?если aob=130 градусов,mob=70 aom=60

Показать ответ

Ответ:

ДевочКаНауКи

27.03.2023 13:31

Пусть угол А=2а, то есть биссектриса делит его на два угла, равным а, аналогично с углом В (2в) и углом С (2с).

Рассматриваем треугольник АВО и треугольник ОВС:

По т. о сумме углов треугольника в треугольнике АВО:

110+а+в=180,

в треугольнике ОВС:

с+в+110=180.

Приравниваем, получаем:

110+а+в=110+с+в

а=с

Значит, 2а=2с, а значит, угол С равен углу А, следовательно треугольник АВС - равнобедренный с основание АС.

Дальше:

угол АОС = 360-110-110= 140.

Треугольник АОС, по т. о сумме углов треугольника:

а+с+140=180, но т.к. а=с:

2а+140=180

2а=40, значит угол А=угол С=40.

Тогда угол В по т. о сумме углов трегольника: 180-40-40=100.

0,0(0 оценок)

Ответ:

natamelnichenko

08.01.2020 22:43

Возможно, так:

Проводим высоту к основанию. Т.к. треугольник равнобедренный, высота будет делить основание пополам. Боковая сторона равна х.

По т. Пифагора в любом маленьком треугольнике получаем:

h²+144=x²

h=√(x²-144)

Находим площадь трегуольника:

s=½*h*24=12 √(x²-144)

По формуле: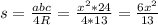 $s=\frac{abc}{4R} = \frac{x^2*24}{4*13}=\frac{6x^2}{13}$

Получем,что

$\frac{6x^2}{13} = 12\sqrt{x^2-144}$

$\frac{x^2}{13} = 2\sqrt{x^2-144}$

$x^2=26\sqrt{x^2-144}$

Возводим в квадрат:

х⁴=676х²-97344

х⁴-676х²+97344=0

Решаем с переменной х².

Дискриминант: 676²-4*97344=456976-389376=260²

х²(1)=468, х(1)=6√13

х²(2)=208, х(2)=4√13.

Теперь рассмотрим эти два варианта. Чтобы треугольник был остроугольный, квадрат наибольшей стороны должен быть меньше суммы квадратов двух других сторон. Однако при х= 4√13, сумма квадратов сторона равна: 208+208=416, а квадрат большей стороны: 24*24=576. Значит, такой треугольник будет тупоугольным, что не подходит под условие. Следовательно, х= 6√13

0,0(0 оценок)

Популярные вопросы: Геометрия