Можно ли в плоскости нарисовать n (бесконечно много) углов таким образом, чтобы каждые 143 угл(-ов, -а) имели общую точку, но в то же время можно было найти точку, которая не принадлежит ни одному из n углов?

Да
Нет

В качестве ответа приложи файл с рисунком.

Показать ответ

Ответ:

zaxar3512

24.08.2022 12:45

1) Точка, лежащая на единичной окружности имеет абсциссу, равную косинусу соответствующего угла, а ординату , равную синусу этого угла.

То есть, если точка А лежит на единичной окружности, то её координаты можно записать так: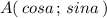 $A(\, cosa\, ;\, sina\, )$ .

Основное тригонометрическое тождество имеет вид: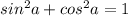 sin^2a+cos^2a=1 .

Поэтому проверяем это тождество для заданных координат.

$A\Big(\, \dfrac{1}{2}\, ;-\dfrac{1}{2}\, \Big):\ \ \Big(\dfrac{1}{2}\Big)^2+\Big(-\dfrac{1}{2}\Big)^2=\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}\ne 1\\\\\\B\Big(\dfrac{\sqrt3}{2}\, ;-\dfrac{1}{2}\, \Big):\ \ \Big(\dfrac{\sqrt3}{2}\Big)^2+\Big(-\dfrac{1}{2}\Big)^2=\dfrac{3}{4}+\dfrac{1}{4}=1\ \ \to \ \ B\in okryznosti\\\\\\C\Big(-\dfrac{\sqrt3}{4}\, ;\, \dfrac{1}{4}\, \Big):\ \ \Big(-\dfrac{\sqrt3}{4}\Big)^2+\Big(\dfrac{1}{4}\Big)^2=\dfrac{3}{16}+\dfrac{1}{16}=\dfrac{1}{4}\ne 1$

$D\Big(\; 0\, ;\, \dfrac{\sqrt2}{2}\Big):\ \ 0^2+\Big(\dfrac{\sqrt2}{2}\Big)^2=0+\dfrac{2}{4}=\dfrac{1}{2}\ne 1$

На единичной окружности лежит точка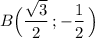 $B\Big(\dfrac{\sqrt3}{2}\, ;-\dfrac{1}{2}\, \Big)$ .

Найдём значение угла, соответствующего точке В, лежащей на единичной окружности.

$cosa=\dfrac{\sqrt3}{2}\ \ ,\ \ sina=-\dfrac{1}{2}\ \ \Rightarrow \ \ \ a=-\dfrac{\pi}{6}+2\pi n\ ,\ n\in Z\\\\tga=\dfrac{sina}{cosa}=-\dfrac{1}{\sqrt3}=-\dfrac{\sqrt3}{3} \\\\ctga=\dfrac{1}{tga}=-\dfrac{3}{\sqrt3}=-\sqrt3$

Смотри рисунок.

$2)\ \ \Delta ABC\ ,\ \ AB=4\ ,\ BC=5\ .\ \angle B=60^\circ \\\\AC^2=4^2+5^2-2\cdot 4\cdot 5\cdot cos60^\circ =41-40\cdot \dfrac{1}{2}=21\ \ ,\ \ \underline {AC=\sqrt{21}\ }\\\\P=4+5+\sqrt{21}=\underline {9+\sqrt{21}\ }\\\\\dfrac{a}{sin\alpha }=2R\ \ \to \ \ R=\dfrac{AC}{2\cdot sin60^\circ }=\dfrac{\sqrt{21}}{2\cdot \frac{\sqrt3}{2}}=\sqrt{\dfrac{21}{3} }=\sqrt7$

$3)\ \ \dfrac{AC}{sinA}=\dfrac{AB}{sinC}=\dfrac{BC}{sinA}=2R\ \ ,\ \ \to \\\\\dfrac{AC}{sinB}=\dfrac{12}{sin50^\circ }=\dfrac{32}{sinA}\ \ ,\ \ \dfrac{AC}{sinB}=\dfrac{12}{0,7660}=\dfrac{32}{sinA}\\\\\\sinA=\dfrac{32\cdot 0,7660}{12}\approx 2,04271$

Так как sin любого угла не превосходит 1, то полученный результат говорит о том, что треугольника с такими размерами не существует. Решения задача не имеет .

0,0(0 оценок)

Ответ:

helenawoy

24.08.2022 12:45

1. а)Уравнение окружности х²+у²=1 этой окружности принадлежит точка В(√3/2;-1/2), т.к. подставляя в уравнение окружности, получим

3/4+1/4=1. остальные не подходят.

б) Эта точка лежит в четвертой четверти, ей соответствует угол 330°, или в радианной мере 11π/6; косинус этого угла равен абсциссе точки, т.е. √3/2, синус - ее ординате, т.е. -1/2, тангенс - отношение синуса к косинусу, т.е. -1/√3=-√3/3, а котангенс обратен тангенсу, и равен -√3. Проверим, например синус sin330°=sin(360°-30°)=sin30°=-1/2

cos330°=cos(360°-30°)=cos(-30°)=cos30°=√3/2

2. по теореме косинусов х²=а²+b²-2ab*cosα; третья сторона х=√(25+16-2*4*5*0.5)=√21/см/; периметр равен 4+5+√21=(9+√21)/см/

Площадь найдем по формуле s=(a*b*sinα)/2=(4*5*sin60°)/2=20√3/см²/

Радиус окружности, описанной около этого треугольника найдем по следствию из теоремы синусов. а/sinα=2R⇒R=a/(2sinα)=

√21/(2√3/2)=√7/cм/

3. по теореме синусов 12/sin50°=32/sinα⇒sinα=32*sin50°/12=

32*0.766/12≈2/043, решений ноль, т.к. не может синус угла быть больше единицы.