Пусть точка, в которой BC пересекает синюю окружность второй раз это K1. На приложенном к условию чертеже она немного левее точки K. Эта окружность проходит через точки A и K, а точка K1 может быть в произвольном месте, но её положение полностью определяет саму окружность.
Поскольку ∠K1KA = 90°; => K1A - диаметр синей окружности.
По этой же причине
∠K1NA = 90°; ∠K1MA = 90°
Поэтому K1M и K1N - перпендикулярны AB и AC, соответственно.
Прежде, чем решать саму задачу, см. рисунки 1 и 2, приложенные к решению. На них решается вс задача, нечто вроде леммы. Я сохранил обозначения, но важно! - что точка H там НЕ является ортоцентром - это произвольная точка на AK. Эта "лемма" доказана там для двух вариантов местоположения точки K1, когда точка H находится внутри отрезка AK. Интересующиеся могут попробовать исследовать другие варианты.
На третьем прилагаемом рисунке - чертеж для решения самой задачи.
Первый шаг - строится окружность по трем точкам A H M и еще одна - на BK1, как на диаметре, эта окружность пройдет через точку M, так как ∠K1MB = 90°. Точка P - это вторая точка пересечения этих окружностей (она есть обязательно, так как уже есть одна - точка M). Второй шаг - по доказанной лемме K1X проходит через точку P и перпендикулярно BH, которая тоже проходит через точку P.
И третье - теперь (вот только теперь!) надо вспомнить, что H - точка пересечения высот (ортоцентр) треугольника ABC, то есть XK1 II AC - обе прямые перпендикулярны BH; => K1XAC - параллелограмм, => XA = K1C;
Доказательство того, что BK1 = AY, аналогичное. => XY = BC; чтд.
Но есть еще более интересная штука. Треугольник K1XY вообще оказывается ЦС-отражением треугольника ABC относительно середины AK1 - центра синей окружности. Интересно, а нет ли тут какой-то гомотетии?
По условию треугольник APD - равносторонний -> AP = AD
ABCD - квадрат -> AB = AD
Следовательно AB = AP -> ΔABP - равнобедренный -> углы при основании равны
∠ABP = ∠APB = = 75°
∠PDC = 90° - 75° = 15°
4)
a) Проводим прямую KL. Отмечаем на ней точку P так, что LP = LK
б) Строим перпендикулярную прямую из точки O к KM. Отмечаем на ней точку H так, чтобы она находилась на одинаковом расстоянии от прямой KM что и точка O
============
Не забывайте сказать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Пусть точка, в которой BC пересекает синюю окружность второй раз это K1. На приложенном к условию чертеже она немного левее точки K. Эта окружность проходит через точки A и K, а точка K1 может быть в произвольном месте, но её положение полностью определяет саму окружность.
Поскольку ∠K1KA = 90°; => K1A - диаметр синей окружности.
По этой же причине
∠K1NA = 90°; ∠K1MA = 90°
Поэтому K1M и K1N - перпендикулярны AB и AC, соответственно.
Прежде, чем решать саму задачу, см. рисунки 1 и 2, приложенные к решению. На них решается вс задача, нечто вроде леммы. Я сохранил обозначения, но важно! - что точка H там НЕ является ортоцентром - это произвольная точка на AK. Эта "лемма" доказана там для двух вариантов местоположения точки K1, когда точка H находится внутри отрезка AK. Интересующиеся могут попробовать исследовать другие варианты.
На третьем прилагаемом рисунке - чертеж для решения самой задачи.
Первый шаг - строится окружность по трем точкам A H M и еще одна - на BK1, как на диаметре, эта окружность пройдет через точку M, так как ∠K1MB = 90°. Точка P - это вторая точка пересечения этих окружностей (она есть обязательно, так как уже есть одна - точка M). Второй шаг - по доказанной лемме K1X проходит через точку P и перпендикулярно BH, которая тоже проходит через точку P.
И третье - теперь (вот только теперь!) надо вспомнить, что H - точка пересечения высот (ортоцентр) треугольника ABC, то есть XK1 II AC - обе прямые перпендикулярны BH; => K1XAC - параллелограмм, => XA = K1C;
Доказательство того, что BK1 = AY, аналогичное. => XY = BC; чтд.
Но есть еще более интересная штука. Треугольник K1XY вообще оказывается ЦС-отражением треугольника ABC относительно середины AK1 - центра синей окружности. Интересно, а нет ли тут какой-то гомотетии?
3) 15°
Объяснение:
3) По условию треугольник APD - равносторонний -> ∠DAP = 60°
ABCD - квадрат -> углы по 90°
∠BAP = 90° - 60° = 30
По условию треугольник APD - равносторонний -> AP = AD
ABCD - квадрат -> AB = AD
Следовательно AB = AP -> ΔABP - равнобедренный -> углы при основании равны
∠ABP = ∠APB =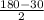 = 75°
= 75°
∠PDC = 90° - 75° = 15°
4)
a) Проводим прямую KL. Отмечаем на ней точку P так, что LP = LK
б) Строим перпендикулярную прямую из точки O к KM. Отмечаем на ней точку H так, чтобы она находилась на одинаковом расстоянии от прямой KM что и точка O
============
Не забывайте сказать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!